Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Déterminer le sommet d'une fonction du second degré à partir de sa forme factorisée - Exercice 3
10 min
25
Soit la fonction définie sur par . On note sa représentation graphique dans un repère orthonormé.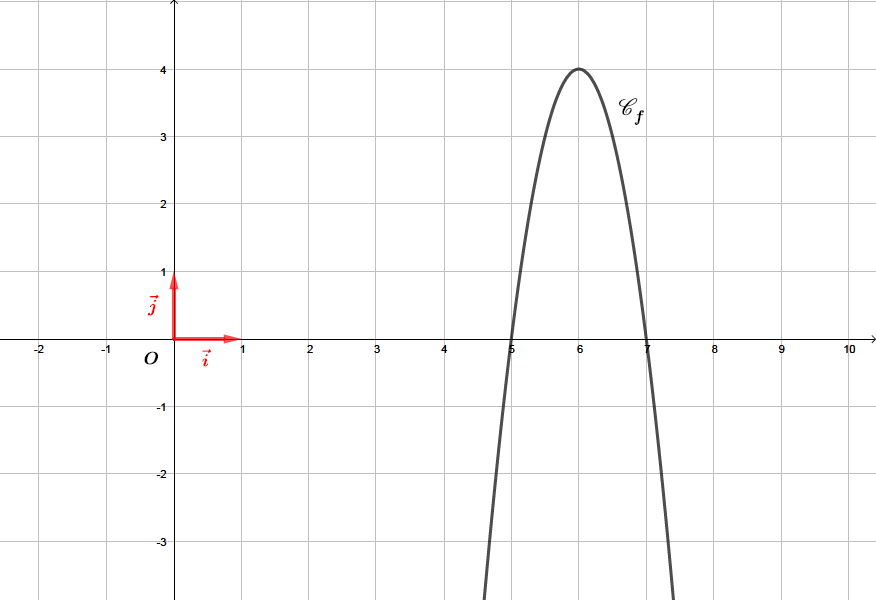

Question 1
Déterminer les points d'intersection de la courbe et de l'axe des abscisses.
Correction
Pour déterminer l’intersection de la courbe de avec l’axe des abscisses, il suffit de résoudre l’équation .
Ainsi :
. Il s'agit ici d'une équation produit nul.
Il faut donc résoudre :
Les points cherchés ont pour coordonnées et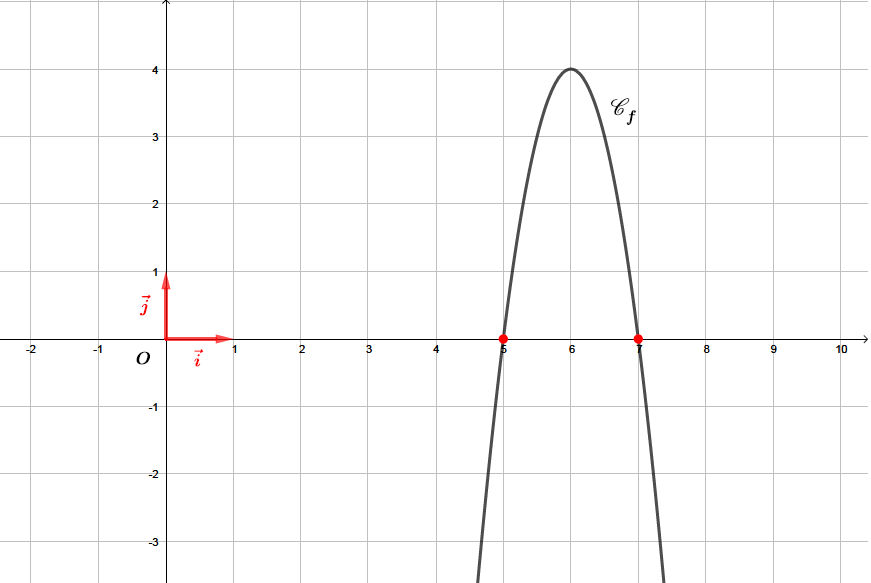
Ainsi :
. Il s'agit ici d'une équation produit nul.
Il faut donc résoudre :
Les points cherchés ont pour coordonnées et

Question 2
Déterminer une équation de l'axe de symétrie de la parabole .
Correction
- La représentation graphique de la fonction où , et sont des constantes réelles avec est une parabole ayant la droite comme axe de symétrie.
L'axe de symétrie admet comme équation , il vient alors :
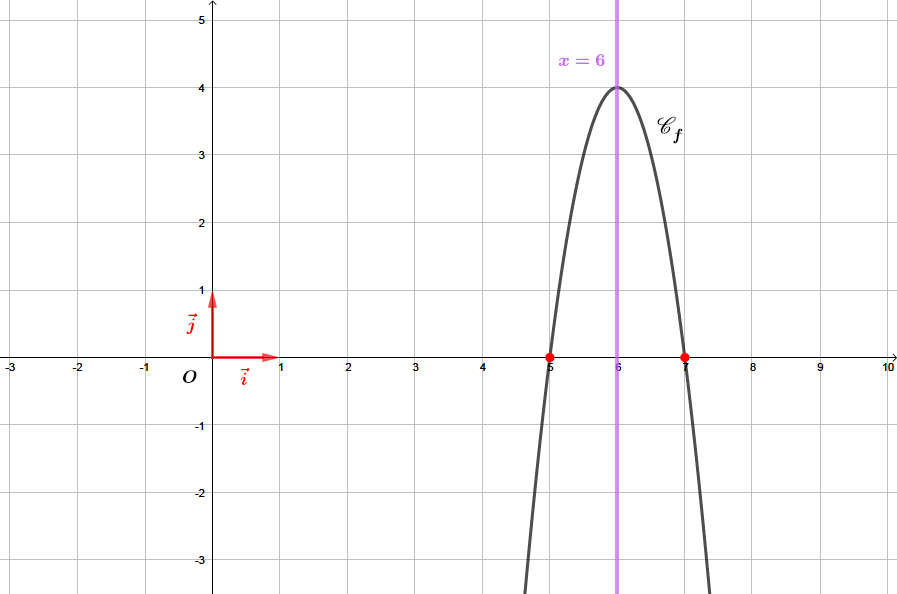
Question 3
Déterminer les coordonnées du sommet de ou encore déterminer les coordonnées de son extremum.
Correction
Déterminer les coordonnées du sommet de ou encore déterminer les coordonnées de son extremum. Il s'agit de deux manières différentes de poser la question.
Le sommet de la parabole appartient à l'axe de symétrie donc son abscisse vaut et son ordonnée vaut
Le sommet de la parabole est donc le point de coordonnées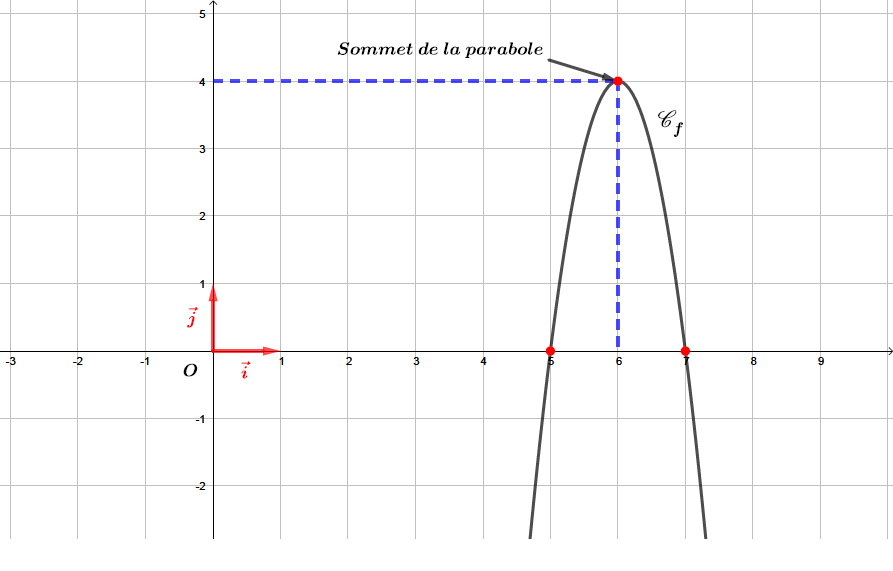
Le sommet de la parabole appartient à l'axe de symétrie donc son abscisse vaut et son ordonnée vaut
Le sommet de la parabole est donc le point de coordonnées

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.