Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Nombres complexes et géométrie sous formes de problèmes - Exercice 4
10 min
15
On considère les points et d'affixes respectifs , , .
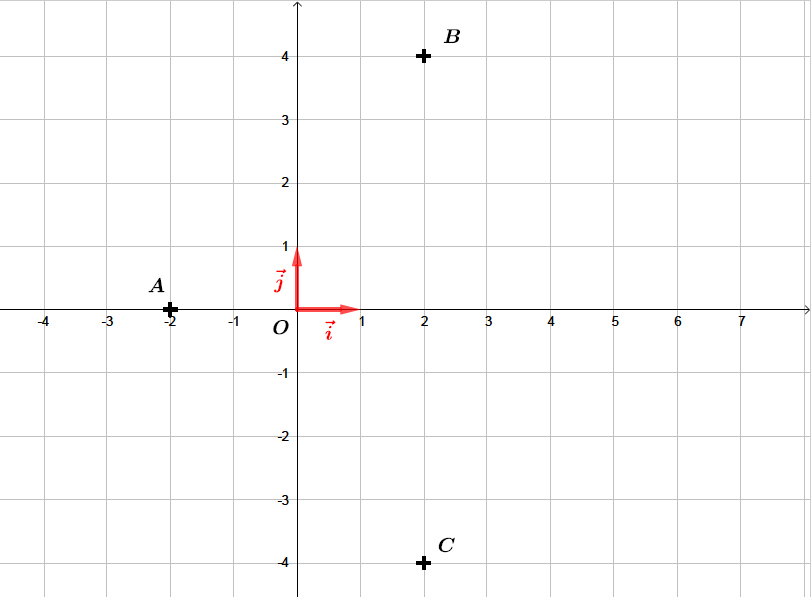
Question 1
Déterminer l'affixe du point tel que soit un parallélogramme.
Correction
Soit l'affixe du point recherché. Pour que soit un parallélogramme, il faut que
Calculons d'une part
équivaut successivement à
Calculons d'autre part
équivaut successivement à
Comme alors résolvons l'équation suivante
d'où
Il vient alors que l'affixe du point doit être égale afin que soit un parallélogramme.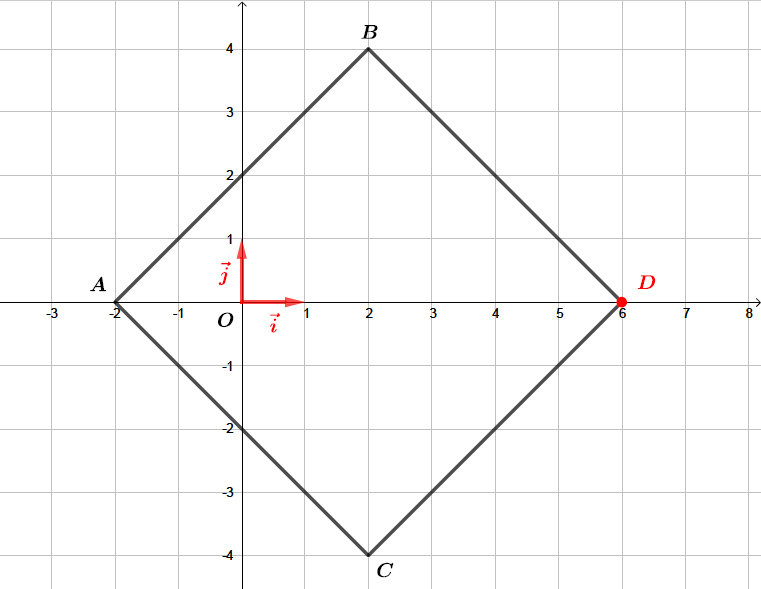
Calculons d'une part
équivaut successivement à
Calculons d'autre part
équivaut successivement à
Comme alors résolvons l'équation suivante
d'où
Il vient alors que l'affixe du point doit être égale afin que soit un parallélogramme.

Question 2
Montrer que est un carré
Correction
On sait maintenant que est un parallélogramme.
Pour que soit un carré, montrons que deux cotés consécutifs sont égaux et qu'il y a un angle droit.
Calculons dans ce cas et donnons son module et son argument.
Comme alors
Nous pouvons en déduire deux choses.
donc
Ainsi d'où
ainsi
Finalement
L'angle est un angle droit.
Finalement est un carré.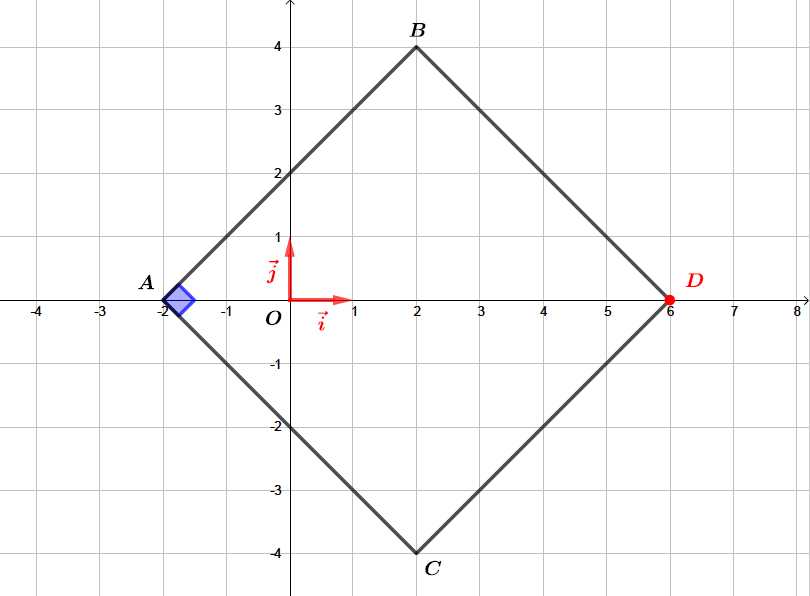
Pour que soit un carré, montrons que deux cotés consécutifs sont égaux et qu'il y a un angle droit.
Calculons dans ce cas et donnons son module et son argument.
Comme alors
Nous pouvons en déduire deux choses.
donc
Ainsi d'où
.
Autrement dit, si est un imaginaire pur dont la partie imaginaire est positive alors l'argument de sera égale à
est un imaginaire pur dont la partie imaginaire est positive , donc d'après le rappel, on a :Autrement dit, si est un imaginaire pur dont la partie imaginaire est positive alors l'argument de sera égale à
ainsi
Finalement
L'angle est un angle droit.
Finalement est un carré.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.