Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 3
25 min
45
On note l'ensemble des nombres complexes.
On munit le plan complexe d'un repère orthonormé direct .
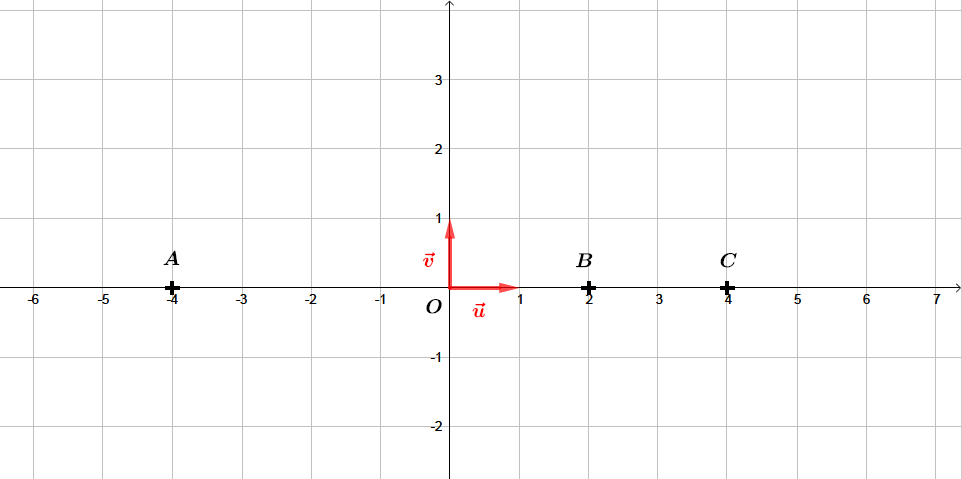
Les points , et ont pour affixes respectives , et .
Question 1
On considère les trois points , et d’affixes respectives , et où est le nombre complexe .
Donner la forme trigonométrique et la forme exponentielle de .
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
- L'écriture exponentielle de est alors
On a donc
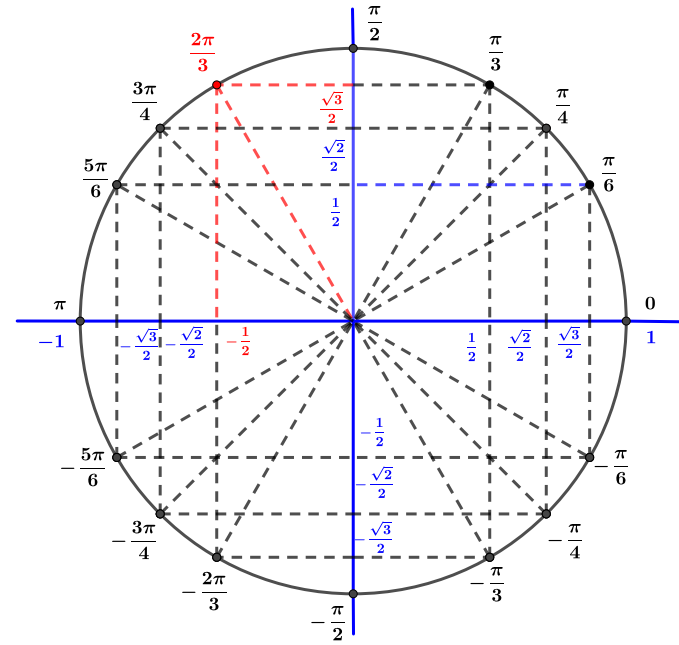
Avec le cercle trigonométrique on en déduit que
Question 2
En déduire les formes algébriques et exponentielles de , et .
Correction
Finalement l'écriture exponentielle de est :
(mesure principale de l'argument)
Finalement l'écriture exponentielle de est :
Finalement l'écriture exponentielle de est :
Question 3
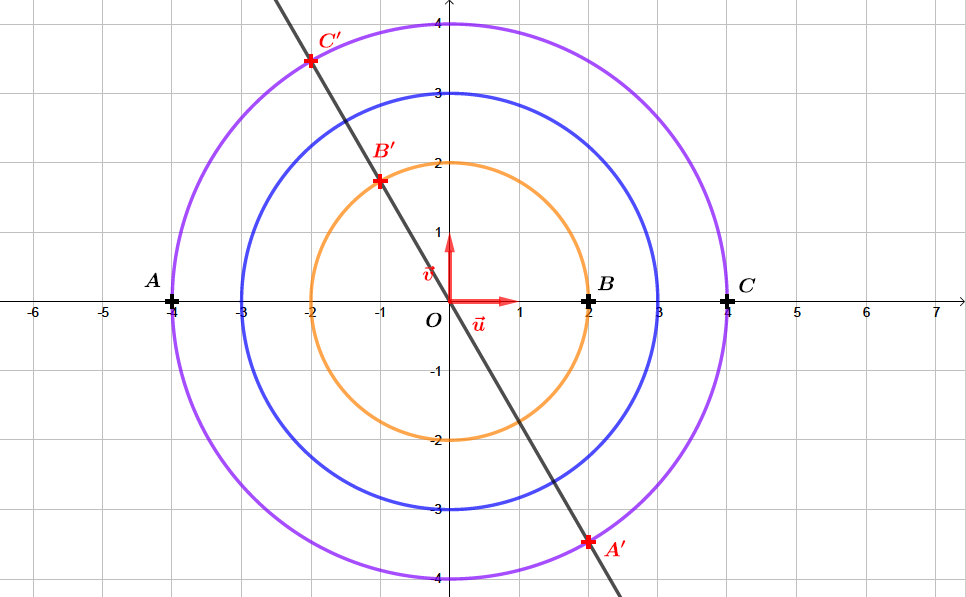
Les points , et ainsi que les cercles de centre et de rayon , et sont représentés sur le graphique ci-dessous.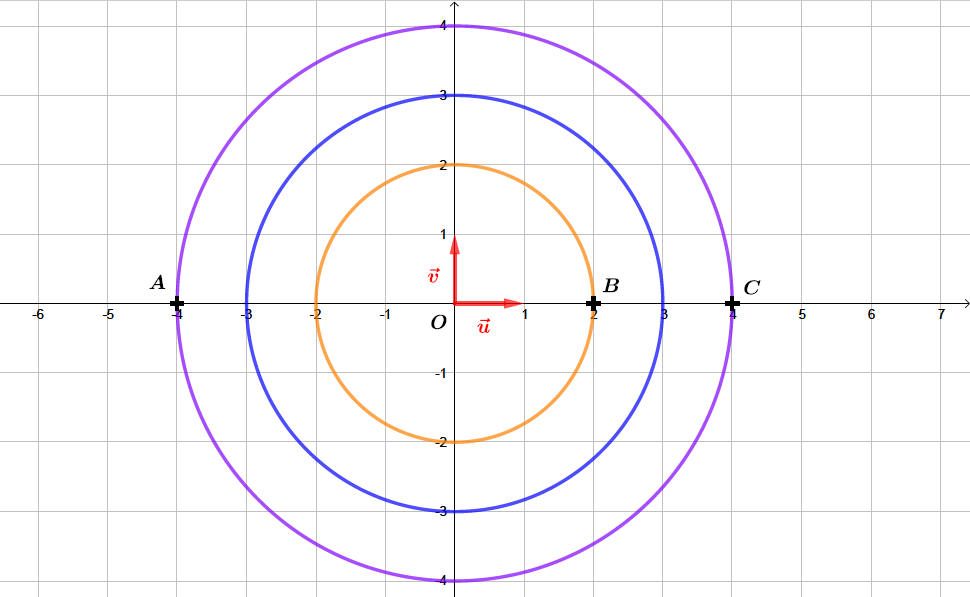

Placer les points , et sur ce graphique.
Correction
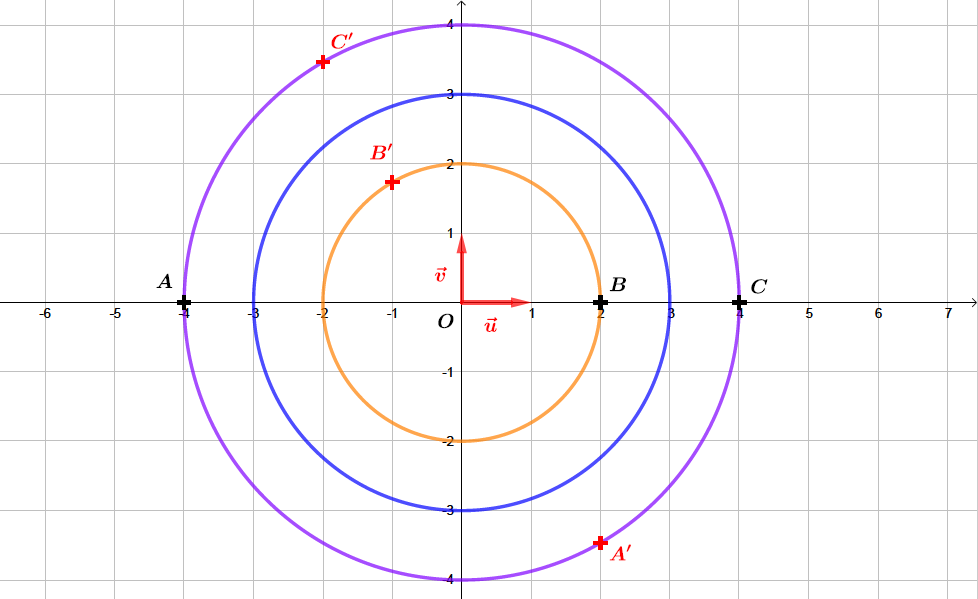
Question 4
Montrer que les points , et sont alignés.
Correction
Il en résulte donc que les points , et sont alignés.
Question 5
On note le milieu du segment , le milieu du segment et le milieu du segment .
Démontrer que le triangle est isocèle.
Correction
Nous allons dans un premier temps calculer les affixes des points , et . On les note respectivement , et .
Nous plaçons les points sur le repère, pour nous donner une idée, quant à la nature du triangle MNP.
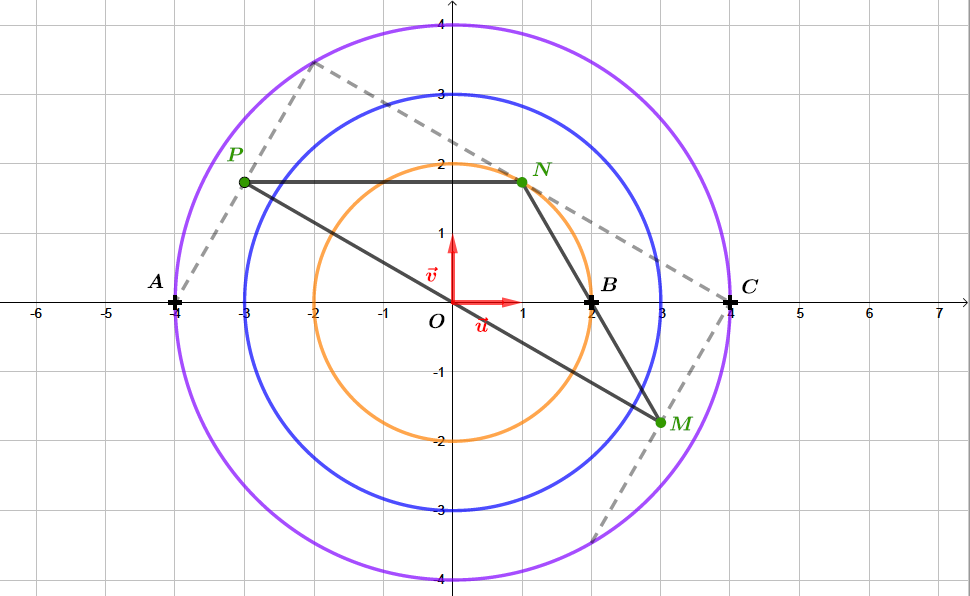 semble isocèle en d’après le dessin.
semble isocèle en d’après le dessin.
La est égale à Nous avons bien . Le triangle est donc bien isocèle en .
Nous plaçons les points sur le repère, pour nous donner une idée, quant à la nature du triangle MNP.

- Soient et deux points d'affixes respectives et .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.