Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Déterminer la forme trigonométrique d'un nombre complexe - Exercice 1
25 min
35
Donner la forme trigonométrique des nombres complexes suivants :
Question 1
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
On a donc
d'où
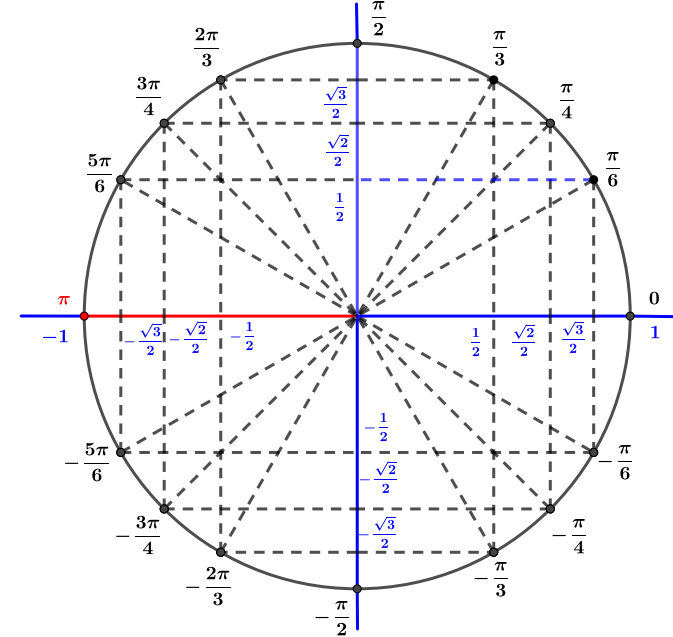
Avec le cercle trigonométrique on en déduit que ou encore
L'écriture trigonométrique de est alors
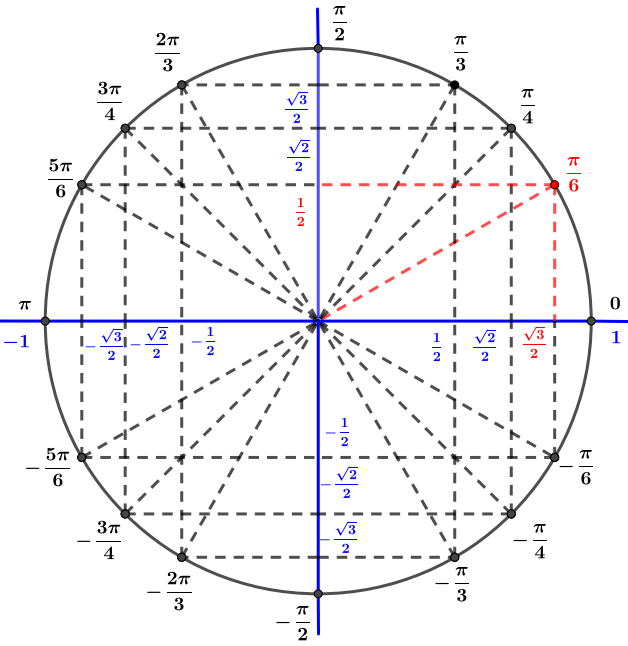
Question 2
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
L'écriture trigonométrique de est alors
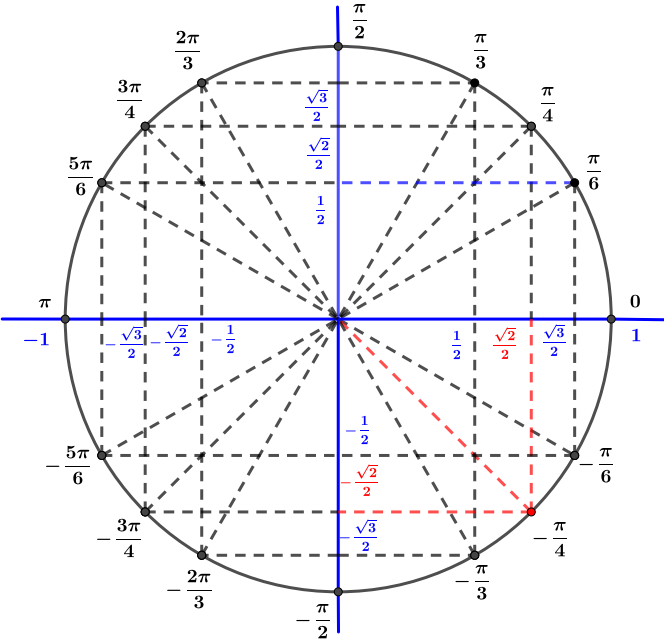
Question 3
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
L'écriture trigonométrique de est alors
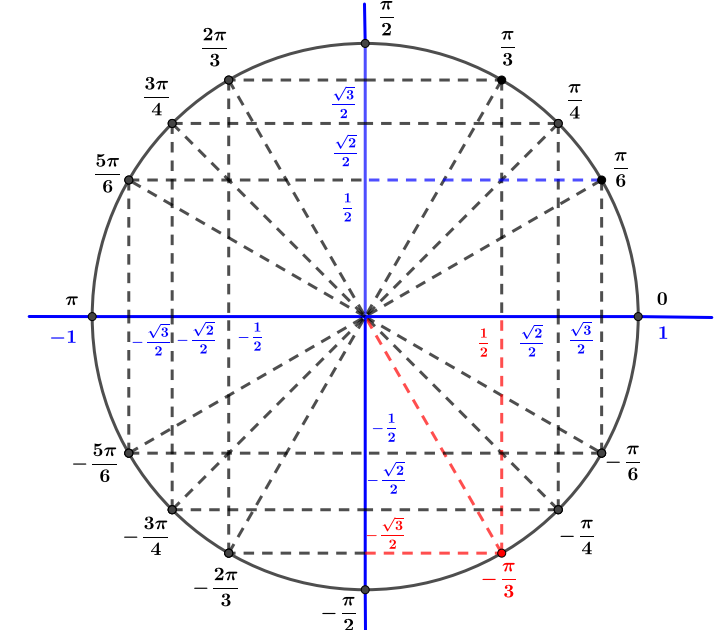
Question 4
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
L'écriture trigonométrique de est alors
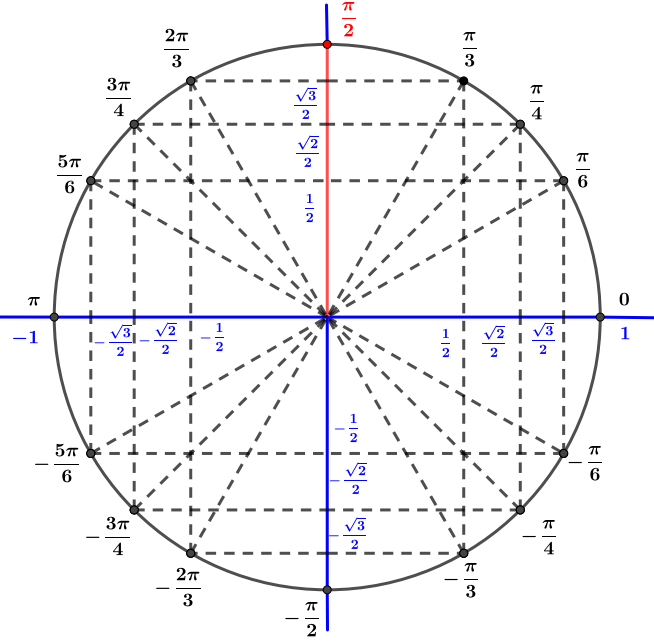
Question 5
Correction
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
On a donc
d'où
Avec le cercle trigonométrique on en déduit que ou encore
L'écriture trigonométrique de est alors
Question 6
Correction
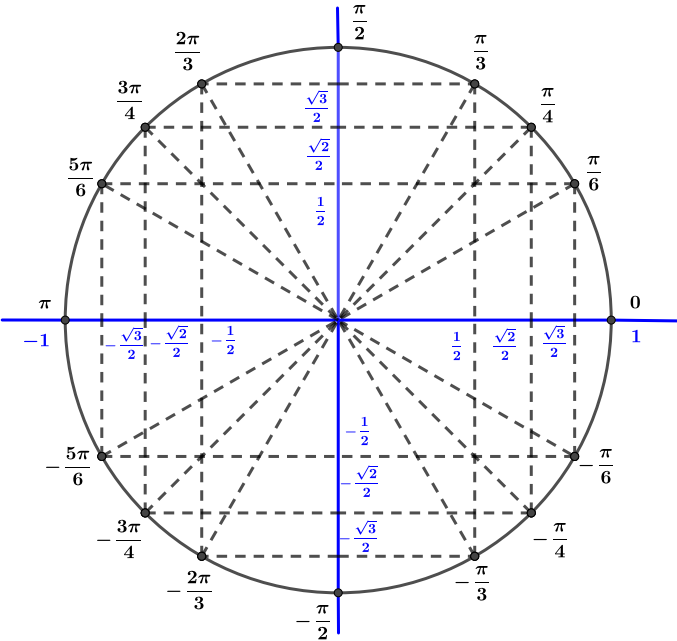
Nous allons donner directement les modules et les arguments du numérateur et du dénominateur car nous avons eu l'occasion de nous exercer avec les exercices précédents (sinon tu peux reprendre la vidéo Module et Argument).
Donc l'écriture exponentielle de est .
Donc l'écriture exponentielle de est .
équivaut successivement à
L'écriture trigonométrique de est alors
Question 7
Correction

Nous allons donner directement les modules et les arguments du numérateur et du dénominateur car nous avons eu l'occasion de nous exercer avec les exercices précédents (sinon tu peux reprendre la vidéo Module et Argument)
Donc l'écriture exponentielle de est .
Donc l'écriture exponentielle de est .
L'écriture trigonométrique de est alors
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.