Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Congruences - Exercice 4
5 min
10
Question 1
Déterminer les valeurs de pour lesquelles est divisible par .
Correction
Dans un premier temps, il nous faut déterminer les restes de la division euclidienne de par .
Les restes possibles dans la division euclidienne de par sont :
Maintenant, en utilisant un tableau des congruences modulo , nous allons déterminer les valeurs de pour lesquelles est divisible par .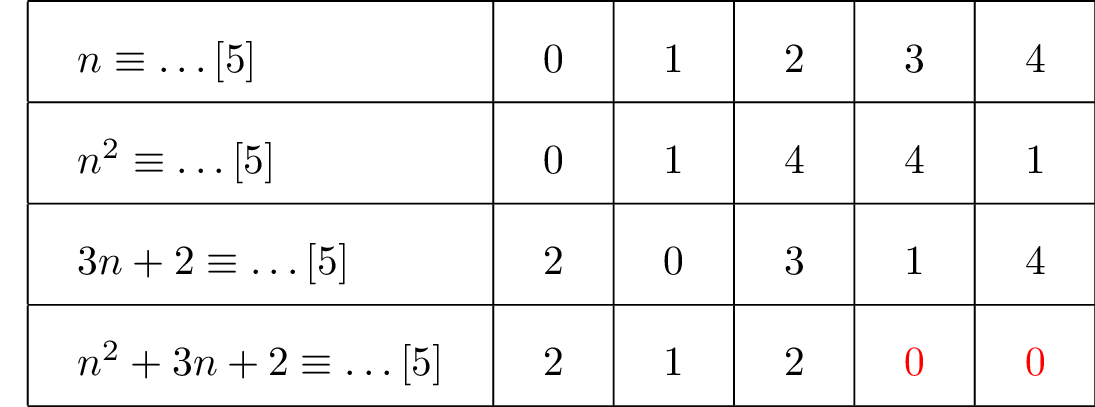 est divisible par si l'on peut écrire : .
est divisible par si l'on peut écrire : .
D'après le tableau des congruences modulo cela est vrai si .
On peut alors conclure que est divisible par pour
Soit un entier relatif et un entier naturel non nul.
On appelle division euclidienne de par , l’opération qui au couple associe le couple tel que : avec s’appelle le dividende, le diviseur, le quotient et le reste.
Nous avons : avec Les restes possibles dans la division euclidienne de par sont :
Maintenant, en utilisant un tableau des congruences modulo , nous allons déterminer les valeurs de pour lesquelles est divisible par .

D'après le tableau des congruences modulo cela est vrai si .
On peut alors conclure que est divisible par pour
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.