Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Effectuer un ajustement exponentiel - Exercice 2

20 min
35
Le tableau suivant donne l’évolution du nombre d’adhérents d’un club de basket de 20142014 à 20192019.
Question 1
On cherche à étudier l’évolution du nombre yy d’adhérents en fonction du rang xx de l’année.
Partie A : un ajustement affine.\text{\red{Partie A : un ajustement affine.}}

Dans le plan muni d’un repère orthogonal d’unités graphiques : 22 cm pour une année sur l’axe des abscisses et 11 cm pour 2020 adhérents sur l’axe des ordonnées, représenter le nuage de points associé à la série (xi;yi)\left(x_i;y_i\right)

Correction
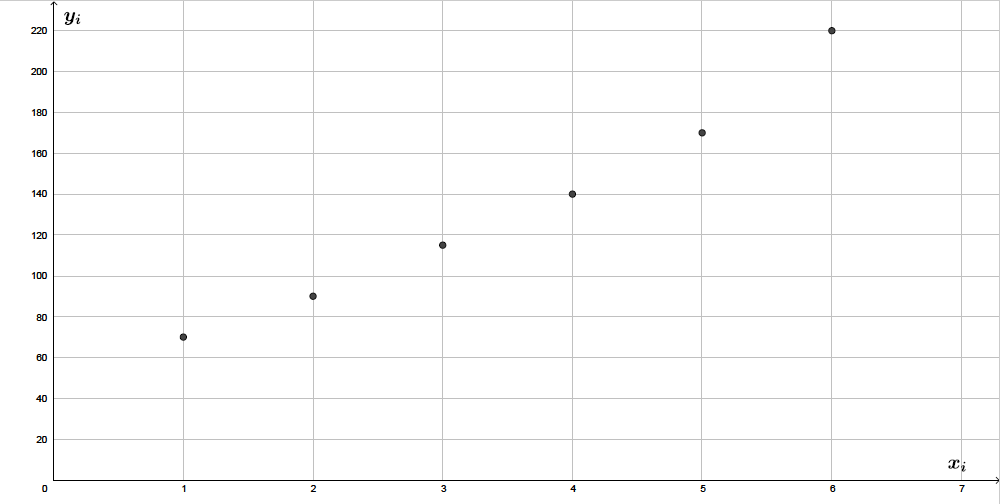
Question 2

Déterminer une équation de la droite d’ajustement de yy en xx obtenue par la méthode des moindres carrés et la tracer sur le graphique précédent. (Les coefficients seront arrondis à l’unité).

Correction
Une équation de la droite (d)\left(d\right) d'ajustement de yy en xx par la méthode des moindres carrés obtenue à l'aide de la calculatrice, est
y=29x+33y=29x+33
(coefficients arrondis à l'unité)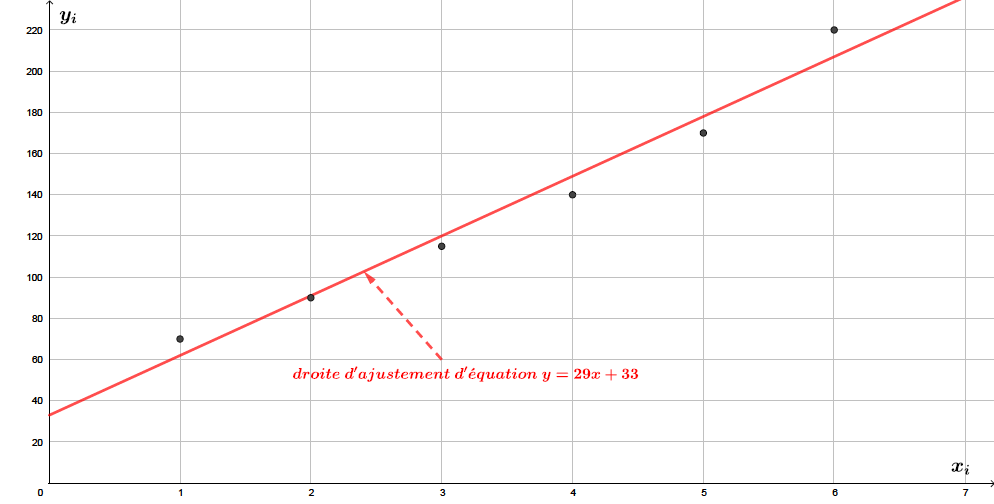
Question 3

En supposant que cet ajustement reste valable pour les années suivantes, donner une estimation du nombre d’adhérents en 20212021.

Correction
L'année 20212021 correspond au rang x=8x=8
L'ajustement affine, d'après la question 22, est : y=29x+33y=29x+33
Il en résulte donc que :
y=29×8+33y=29 \times 8+33
y=232+33y=232+33
Ainsi :
y=265y=265

Avec cet ajustement, nous pouvons prévoir 265265 adhérents en 20212021.
Question 4
Partie A : un ajustement exponentiel.\text{\red{Partie A : un ajustement exponentiel.}}
On pose z=ln⁡(y){\color{blue}{z=\ln\left(y\right)}}

Recopier et compléter le tableau suivant en arrondissant les valeurs de ziz_{i} au millième .

Correction
Nous allons détailler un exemple.
  • Lorsque y=90y=90 alors z=ln⁡(90)z=\ln\left(90\right) ce qui nous donne z≈4,5z\approx 4,5 arrondi à 10−310^{-3} près.
    • Question 5

    Déterminer une équation de la droite d’ajustement de zz en xx obtenue par la méthode des moindres carrés et la tracer sur le graphique précédent. (Les coefficients seront arrondis au millième).

    Correction
    Une équation de la droite (d)\left(d\right) d'ajustement de zz en xx par la méthode des moindres carrés obtenue à l'aide de la calculatrice, est
    z=0,224x+4,044z=0,224x+4,044
    (coefficients arrondis au centième)
    Question 6

    En déduire une approximation du nombre d’adhérents yy en fonction du rang xx de l’année. On vérifiera que y=AeBxy=Ae^{Bx} où AA et BB sont deux réels à déterminer.

    Correction
    Nous savons que z=ln⁡(y)z=\ln\left(y\right) et que z=0,224x+4,044z=0,224x+4,044. Il en résulte donc que :
    ln⁡(y)=0,224x+4,044\ln \left(y\right)=0,224x+4,044
    eln⁡(y)=e0,224x+4,044e^{\ln \left(y\right)} =e^{0,224x+4,044}
    y=e0,224x+4,044y=e^{0,224x+4,044}
    y=e0,224x×e4,044y=e^{0,224x} \times e^{4,044} . Or : e4,044≈57,041e^{4,044} \approx 57,041
    Ainsi :
    y=57,041e0,224xy=57,041e^{0,224x}

    Par identification, on a alors : A=57,041A=57,041 et B=0,224B=0,224
    Question 7

    En prenant l’approximation y≈57,1e0,224xy\approx 57,1e^{0,224x} et en supposant qu’elle reste valable pour les années suivantes, donner une estimation du nombre d’adhérents en 20212021.

    Correction
    On nous donne l'ajustement exponentiel y≈57,1e0,224xy\approx 57,1e^{0,224x}
    L'année 20212021 correspond au rang x=8x=8
    Il vient alors que :
    y≈57,1e0,224×8y\approx 57,1e^{0,224\times8}
    Ainsi :
    y≈343y\approx 343

    Avec cet ajustement exponentiel, nous pouvons prévoir 343343 adhérents en 20212021.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.