Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 3
40 min
65
Partie A .
Question 1
Soit la fonction définie sur par .
Déterminer la limite de la fonction en et en .
Correction
D'une part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Donc :
D'autre part : . Au voisinage de , un polynôme est équivalent à son monôme de plus haut degré. Autrement dit, on n'étudie que la limite du monôme de plus haut degré.
Donc :
Question 2
Déterminer le tableau de variation de la fonction sur .
Correction
est dérivable sur .
Il vient alors que :
.
Il s'agit d'une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.
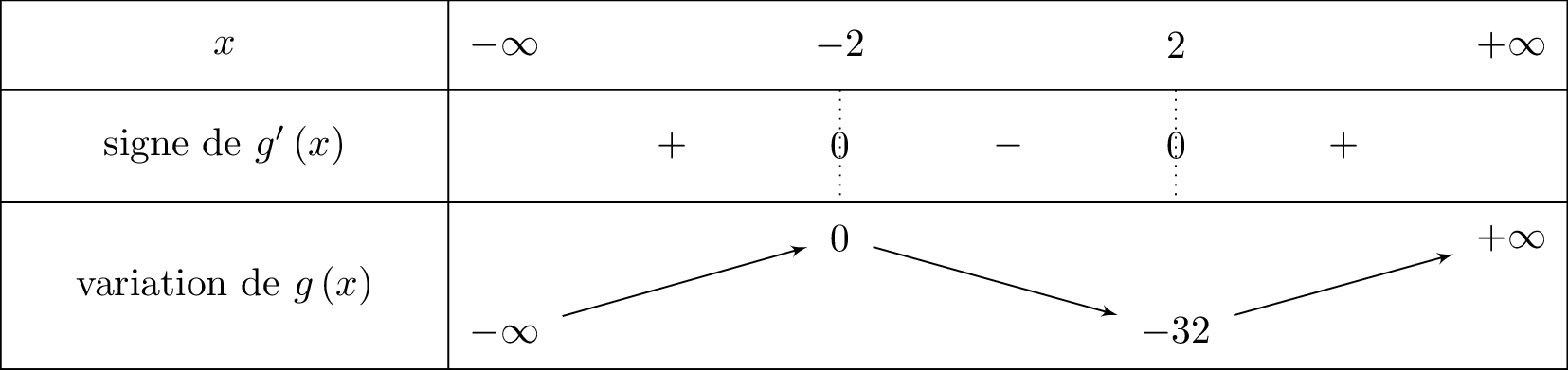 De plus:
De plus:
ainsi
ainsi
Il vient alors que :
.
Il s'agit d'une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.

ainsi
ainsi
Question 3
Démontrer que l'équation admet deux solutions sur .
On notera la solution sur l'intervalle .
On notera la solution sur l'intervalle .
Correction
Nous faisons apparaître les deux zéro recherchés dans le tableau de variation donnée. Il vient alors que : 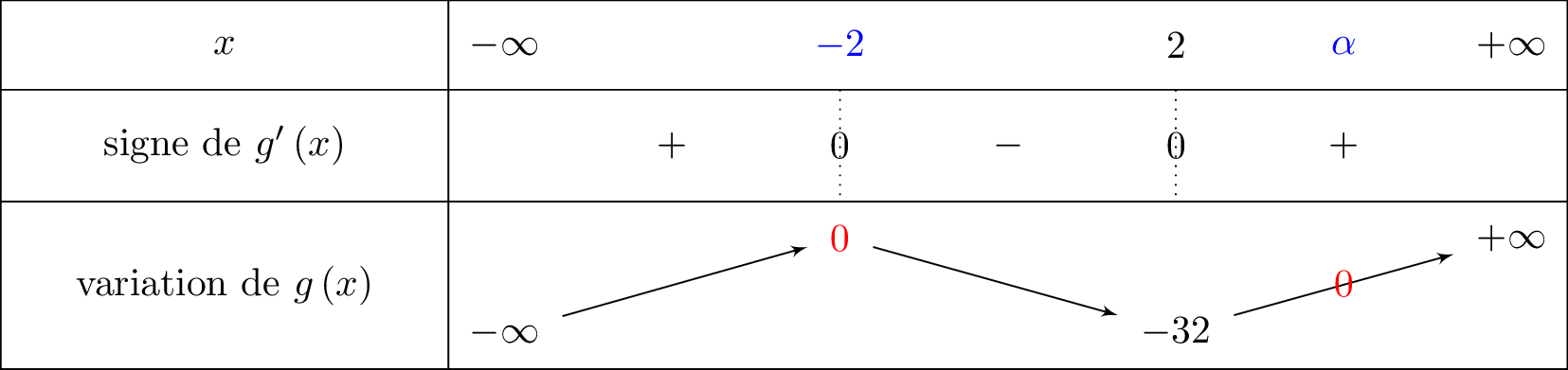 D'après la question , nous avons vu que . Il s'agit de la première solution et unique solution sur l'intervalle .
D'après la question , nous avons vu que . Il s'agit de la première solution et unique solution sur l'intervalle .
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .

Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Question 4
Déterminer une valeur exacte de .
Correction
A la calculatrice, on vérifie que :
On en déduit que :
On en déduit que :
Question 5
Déterminer le signe de la fonction sur .
Correction

Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 6
Partie B
La fonction est définie sur par . On note sa représentation graphique dans le repère orthogonal.
La fonction est définie sur par . On note sa représentation graphique dans le repère orthogonal.
Etudiez les limites de aux bornes de l'ensemble de définition. Que peut-on en déduire graphiquement?
Correction
D'une part calculons la limite de en .
On va factoriser le numérateur par le monôme de plus haut degré c'est à dire par et le dénominateur par le monôme de plus haut degré c'est à dire par .
Il vient :
Ainsi : par quotient :
D'autre part calculons la limite de en .
par quotient :
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
On va factoriser le numérateur par le monôme de plus haut degré c'est à dire par et le dénominateur par le monôme de plus haut degré c'est à dire par .
Il vient :
Ainsi : par quotient :
D'autre part calculons la limite de en .
par quotient :
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
Question 7
On rappelle que :
Démontrer que pour tout réel de , on a : .
Correction
On reconnait la forme avec et
Ainsi : et
Il vient alors que :
équivaut successivement à :
. On factorise le numérateur par
.
Ainsi :
Ainsi : et
Il vient alors que :
équivaut successivement à :
. On factorise le numérateur par
.
Ainsi :
Question 8
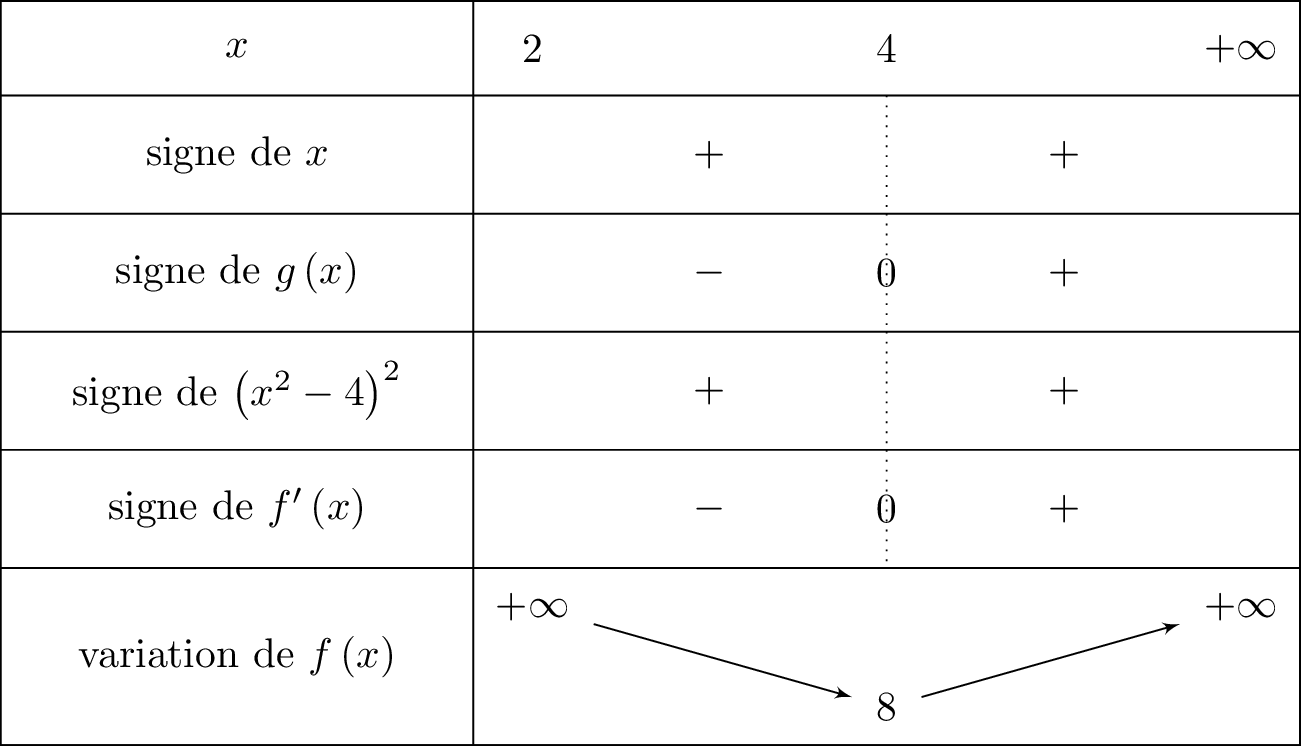
Etablir le tableau de variations de la fonction sur .
Correction
Pour tout réel , on vérifie aisément que et que .
Il en résulte donc que le signe de dépend alors du signe de la fonction .
Or d'après la question , nous connaissons le signe de la fonction que l'on rappelle ci-dessous.
 . Il en résulte donc que :
. Il en résulte donc que :
 De plus : ainsi
De plus : ainsi
Il en résulte donc que le signe de dépend alors du signe de la fonction .
Or d'après la question , nous connaissons le signe de la fonction que l'on rappelle ci-dessous.

- si alors
- si alors

Question 9
On note la droite d'équation : .
Etudier la position relative entre la courbe et la droite sur l'intervalle .
Correction
Soit la fonction telle que : . Etudions le signe de .
Ainsi :
Pour tout réel , on vérifie facilement que et .
Il en résulte donc que :
Ainsi : et donc .
Géométriquement, cela signifie que la courbe représentative de la fonction est au-dessus de la droite .
Ainsi :
Pour tout réel , on vérifie facilement que et .
Il en résulte donc que :
Ainsi : et donc .
Géométriquement, cela signifie que la courbe représentative de la fonction est au-dessus de la droite .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.