Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Comment reconnaître qu'une fonction admet une asymptote horizontale ou une asymptote verticale - Exercice 2
15 min
25
Calculer les limites suivantes et que peut-on en déduire graphiquement ?
Question 1
qui s'écrit également
Correction
- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
, Ici on a le numérateur vaut et il est négatif et le dénominateur s'approche de de manière positive, lorsque tend vers avec strictement supérieur à .
Le numérateur est négatif et le dénominateur est positif donc le quotient tend vers .
Le numérateur est négatif et le dénominateur est positif donc le quotient tend vers .
On peut expliquer le fait que de la manière suivante :
Nous avons dressé le signe de la fonction ci dessous :
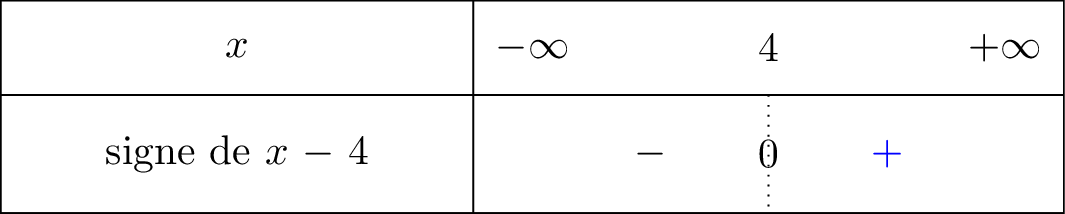 signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
Nous avons dressé le signe de la fonction ci dessous :

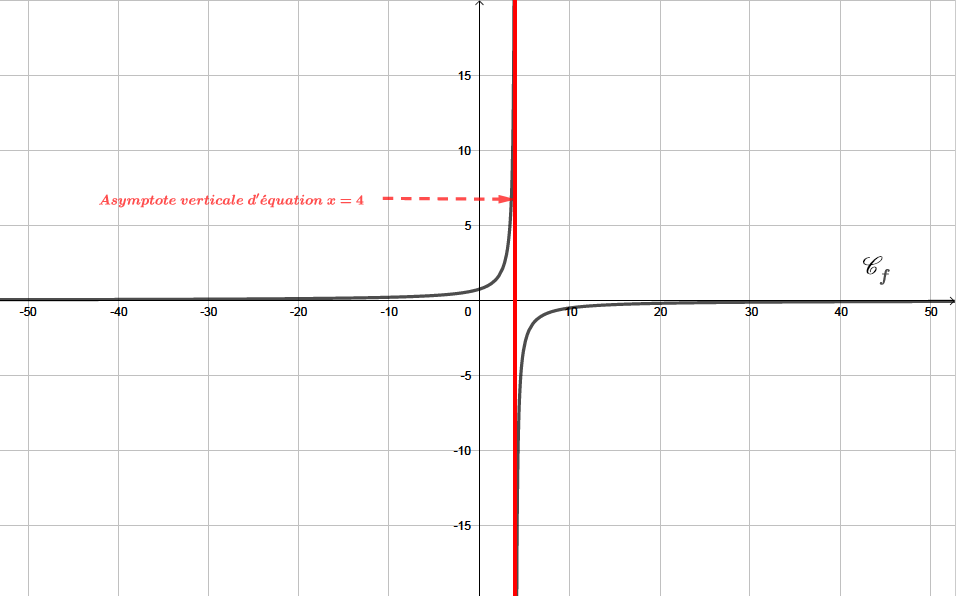
Question 2
qui s'écrit également
Correction
- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
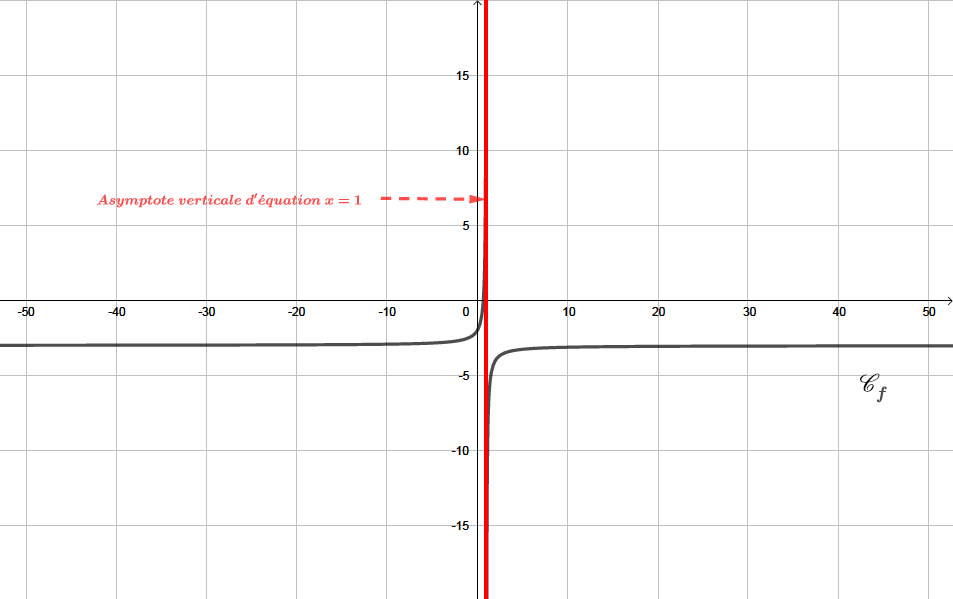
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
, Ici on a le numérateur vaut donc positif et le dénominateur s'approche de de manière positive, lorsque tend vers avec strictement inférieur à .
Le numérateur est positif tout comme le dénominateur donc le quotient tend vers .
Le numérateur est positif tout comme le dénominateur donc le quotient tend vers .
On peut expliquer le fait que de la manière suivante :
Nous avons dressé le signe de la fonction ci dessous :
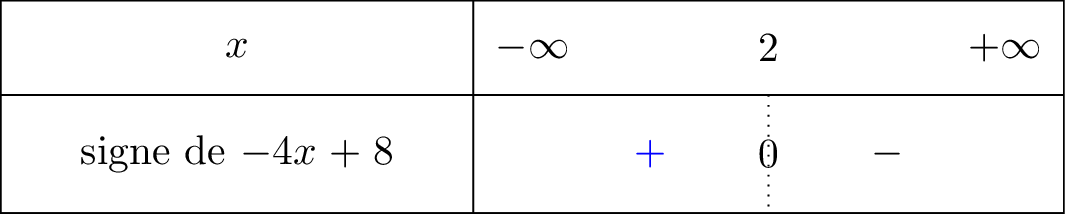 signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
Nous avons dressé le signe de la fonction ci dessous :

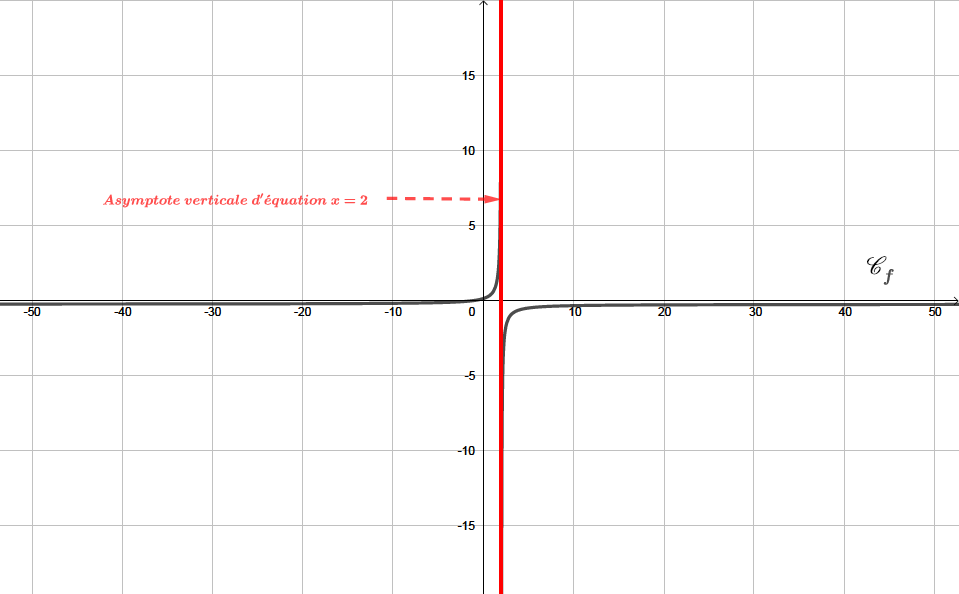
Question 3
qui s'écrit également
Correction
- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
, Ici on a le numérateur vaut donc positif et le dénominateur s'approche de de manière positive, lorsque tend vers avec strictement inférieur à .
Le numérateur est positif tout comme le dénominateur donc le quotient tend vers .
Le numérateur est positif tout comme le dénominateur donc le quotient tend vers .
On peut expliquer le fait que de la manière suivante :
Nous avons dressé le signe de la fonction ci dessous :
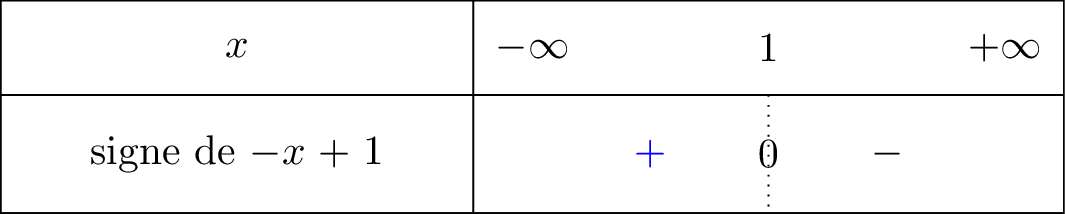 signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
signifie que tend vers mais avec , donc lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que .
Nous avons dressé le signe de la fonction ci dessous :

Question 4
qui s'écrit également
Correction
Dans un premier temps, nous allons étudier le signe du dénominateur .
On vérifie facilement que : ; et .
Le tableau de signe de est alors :
 Il en résulte donc que :
Il en résulte donc que :
par quotient .
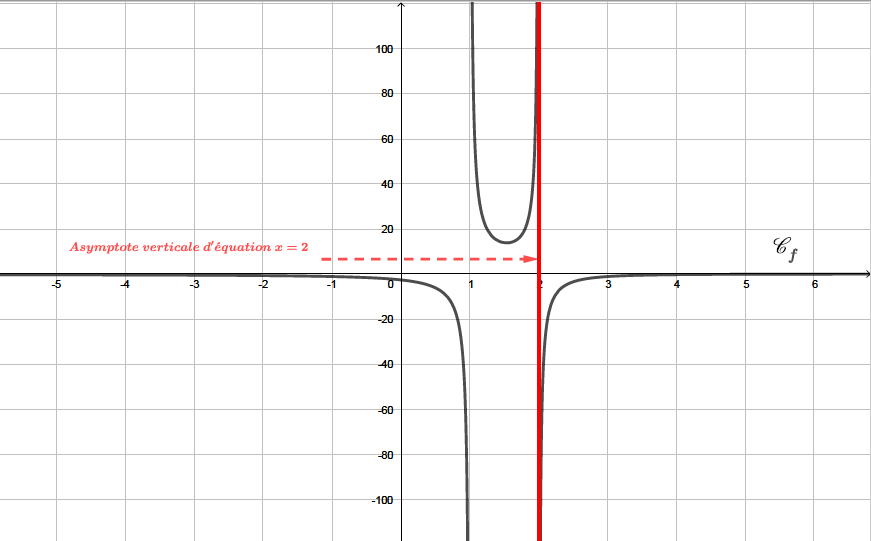
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
On vérifie facilement que : ; et .
Le tableau de signe de est alors :

- Si alors la fonction admet une asymptote verticale d'équation
- Si alors la fonction admet une asymptote verticale d'équation
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
, Ici on a le numérateur vaut donc négatif et le dénominateur s'approche de de manière négative, lorsque tend vers avec strictement inférieur à .
Le numérateur est négatif tout comme le dénominateur donc le quotient tend vers .
Le numérateur est négatif tout comme le dénominateur donc le quotient tend vers .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.