Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : 2ème partie - Exercice 1
30 min
50
On considère la fonction définie sur par :
Question 1
Calculer sur
Correction
Question 2
Etudier le signe de et dresser le tableau de variation de
Correction
Etudions le signe de
Sur l'intervalle on peut donc en déduire que
Par conséquent est positive sur
Etudions la variation de
est positive sur on peut donc conclure que la fonction est strictement croissante sur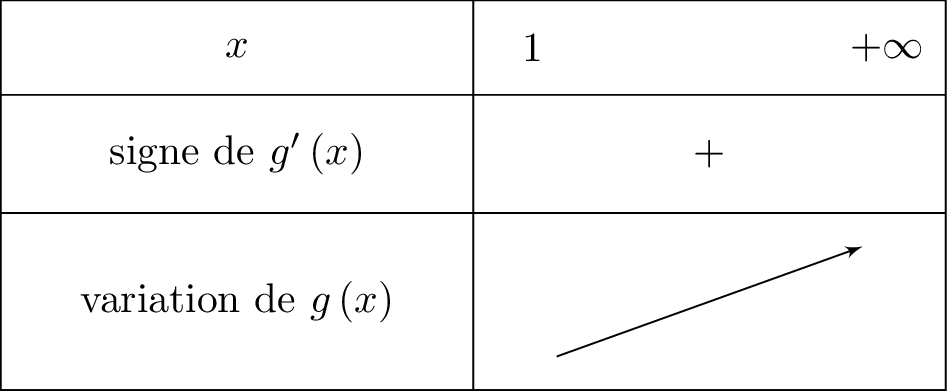
Sur l'intervalle on peut donc en déduire que
Par conséquent est positive sur
Etudions la variation de
est positive sur on peut donc conclure que la fonction est strictement croissante sur

Question 3
Résoudre l’équation dans
Correction
car
Or , donc la solution de l'équation est :
Question 4
En déduire que si et seulement si
Correction
car
Finalement : si et seulement si
Question 5
On considère la fonction définie sur par :
Déterminer la limite de en
Correction
Question 6
On appelle la fonction dérivée de la fonction sur l’intervalle
Montrer que pour tout nombre réel de l’intervalle
Correction
Ici on reconnaît la forme avec , et
Ainsi , et
Il vient alors que :
Nous allons factoriser par , ce qui nous donne :
Finalement :
Question 7
Étudier le signe de sur et en déduire le tableau de variations de sur [
Correction
D'après la question précédente nous savons que :
D'après la question , nous avons aussi montrer que si et seulement si
Autrement dit :
si on a si on a si on a De plus, si alors .
Nous traduisons cela dans le tableau de variation de .
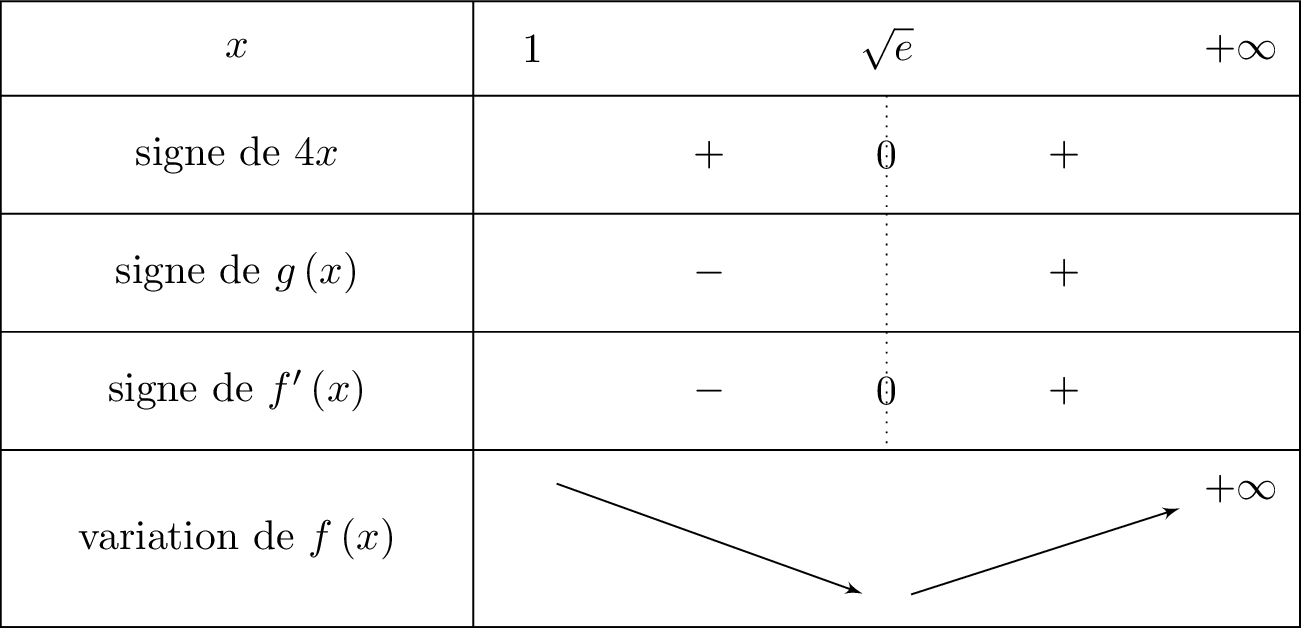
D'après la question , nous avons aussi montrer que si et seulement si
Autrement dit :
Nous traduisons cela dans le tableau de variation de .

Question 8
Montrer que, dans l’intervalle l’équation admet une solution unique notée
Correction
Nous commençons par calculer les valeurs et .
On reprend le tableau de variation fait à la question précédente. On fera apparaitre dans le tableau le zéro que l'on recherche.
On reprend le tableau de variation fait à la question précédente. On fera apparaitre dans le tableau le zéro que l'on recherche.
- Sur , la fonction est continue et strictement croissante. De plus, et
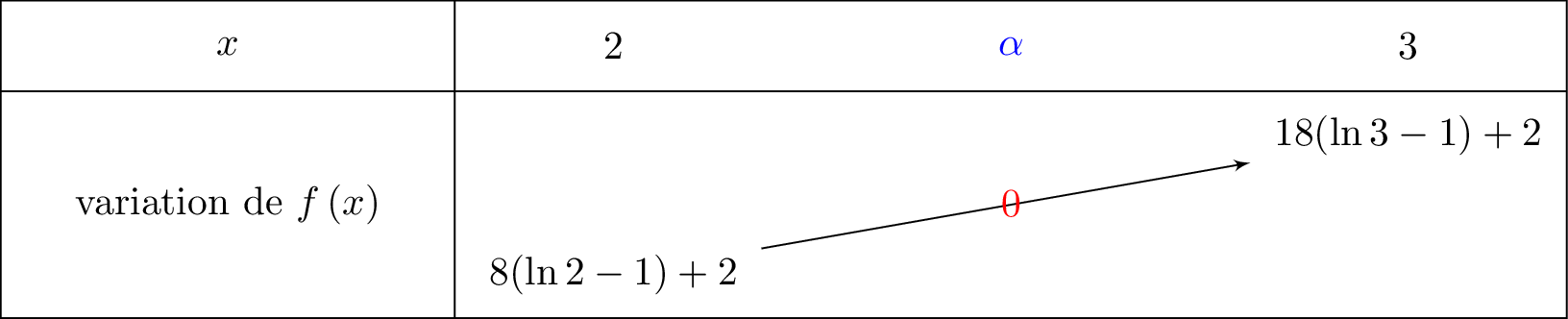
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Question 9
Déterminer un encadrement d’amplitude de
Correction
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.