Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : 1ère partie - Exercice 2
25 min
45
Question 1
On considère la fonction dont la courbe représentative est représentée ci-dessous dans le plan muni d'un repère orthonormal.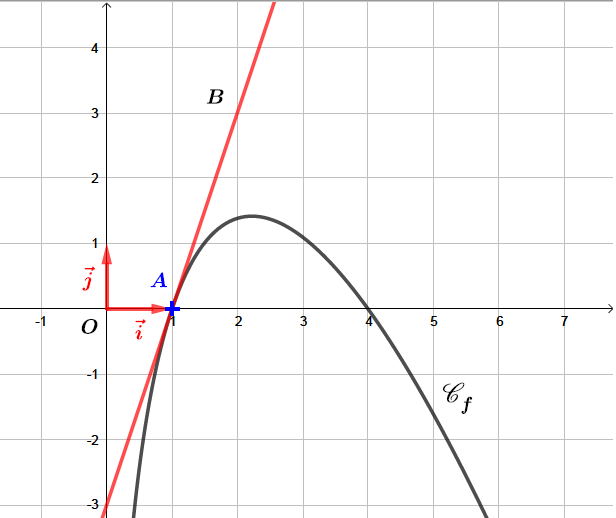
La courbe passe par le point et admet la droite pour tangente à la courbe
Pour tout réel de , où et sont deux réels.

La courbe passe par le point et admet la droite pour tangente à la courbe
Pour tout réel de , où et sont deux réels.
Calculer en fonction de et .
Correction
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Question 2
Sans justifier et par lecture graphique, donner et
Correction
Pour rappel, correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . 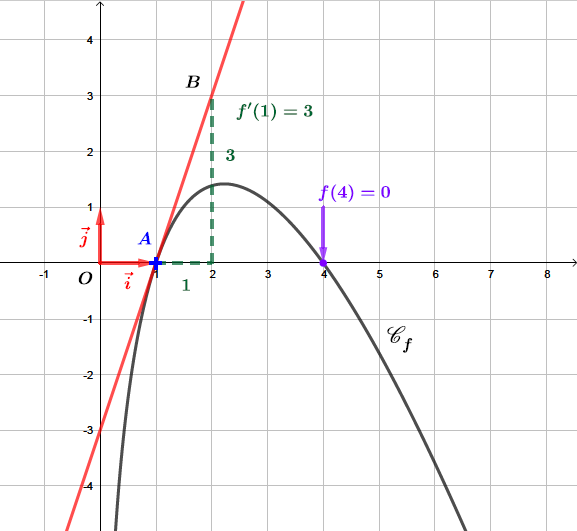
A l'aide du graphique on peut donc conclure que: et

A l'aide du graphique on peut donc conclure que: et
Question 3
Justifier que et sont solutions du système suivant:
Correction
On à déterminer à la question précédente que : et que
Or et On peut donc en déduire :
Or et On peut donc en déduire :
Question 4
Déterminer et .
Correction
Il nous faut résoudre le système suivant :
. Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la deuxième ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la première ligne .
. Maintenant, la première ligne est une équation à une inconnue que nous allons résoudre :
Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la deuxième ligne le par . Il vient :
Le couple solution du système est alors :
. Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la deuxième ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la première ligne .
. Maintenant, la première ligne est une équation à une inconnue que nous allons résoudre :
Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la deuxième ligne le par . Il vient :
Le couple solution du système est alors :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.