Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 2
55 min
80
On considère la suite à valeurs réelles définie par et, pour tout entier naturel , .
Question 1
Partie A: Conjectures
Les premières valeurs de la suite ont été calculées à l’aide d’un tableur dont voici une capture d’écran :
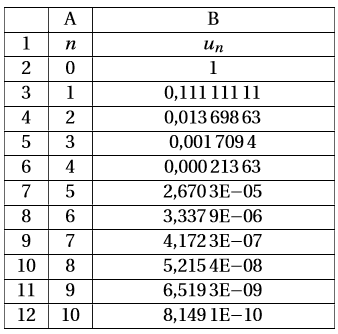
Quelle formule peut-on entrer dans la cellule B3 et copier vers le bas pour obtenir les valeurs des premiers termes de la suite ?
Correction
Il nous faut entrer la formule
B2 / (B2)
Question 2
Quelle conjecture peut-on faire sur les variations de la suite ?
Correction

Question 3
Quelle conjecture peut-on faire sur la limite de la suite ?
Correction

Question 4
Écrire un algorithme calculant .
Correction
Variables : un entier et un réel
prend la valeur
Pour allant de à
prend la valeur
Fin Pour
Afficher
prend la valeur
Pour allant de à
prend la valeur
Fin Pour
Afficher
Question 5
Partie B : Étude générale
On considère la suite à valeurs réelles définie par et, pour tout entier naturel , .
On considère la suite à valeurs réelles définie par et, pour tout entier naturel , .
Démontrer par récurrence que, pour tout entier naturel , .
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que et que .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
et donc . Ainsi le numérateur et le dénominateur .
De ce fait :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Etape d'initialisation
On sait que et que .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
et donc . Ainsi le numérateur et le dénominateur .
De ce fait :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Question 6
Étudier les variations de la suite .
Correction
Pour étudier les variations de la suite , nous allons étudier le signe de .
Ainsi :
. Nous allons factoriser par
. Nous allons maintenant tout mettre au même dénominateur.
Nous avons vu à la question , que pour tout entier naturel ,
Ainsi, on vérifie facilement que et que .
Finalement :
Il en résulte donc que .
La suite est donc décroissante.
Ainsi :
. Nous allons factoriser par
. Nous allons maintenant tout mettre au même dénominateur.
Nous avons vu à la question , que pour tout entier naturel ,
Ainsi, on vérifie facilement que et que .
Finalement :
Il en résulte donc que .
La suite est donc décroissante.
Question 7
La suite est-elle convergente ? Justifier.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 8
Partie C: Recherche d’une expression du terme général
On définit la suite en posant, pour tout entier naturel ,
On définit la suite en posant, pour tout entier naturel ,
Exprimer en fonction de .
Correction
Question 9
Démontrer que la suite est une suite géométrique de raison dont on déterminera le premier terme.
Correction
. Or
Ainsi la suite est géométrique de raison et de premier terme donc
Question 10
Exprimer en fonction de .
Correction
- L'expression de en fonction de est donnée par la formule
Question 11
Justifier que, pour tout entier naturel , .
Correction
D'après la question , nous avons vu que
Or nous savons d'après la question que :
Ainsi :
Or nous savons d'après la question que :
Ainsi :
Question 12
Déterminer la limite de la suite .
Correction
- Si alors .
- Si alors .
Finalement :
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.