Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 5
20 min
40
Soit la suite numérique définie sur par et pour tout entier naturel non nul , .
Question 1
Pour calculer et afficher le terme , on propose l'algorithme ci-dessous.
Compléter les lignes de l'algorithme où figurent des points de suspension.
Variables
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que ....
Affecter à la valeur...
Affecter à la valeur...
Fin tant que
Sortie
Afficher la valeur
Compléter les lignes de l'algorithme où figurent des points de suspension.
Variables
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que ....
Affecter à la valeur...
Affecter à la valeur...
Fin tant que
Sortie
Afficher la valeur
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que ....
Affecter à la valeur...
Affecter à la valeur...
Fin tant que
Sortie
Afficher la valeur
Correction
Variables
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que
Affecter à la valeur
Affecter à la valeur
Fin tant que
Sortie
Afficher la valeur .
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que
Affecter à la valeur
Affecter à la valeur
Fin tant que
Sortie
Afficher la valeur .
Question 2
Comment faudrait-il modifier cet algorithme pour qu'il calcule et affiche tous les termes de la suite de jusqu'à ?
Correction
Variables
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que
Affecter à la valeur
Affecter à la valeur
Fin tant que
est un entier naturel; est un réel
Initialisation
Affecter à la valeur .
Affecter à la valeur .
Traitement
Tant que
Affecter à la valeur
Affecter à la valeur
Fin tant que
Question 3
Soit la suite numérique définie sur par et pour tout entier naturel ,
Compléter le tableau suivant :
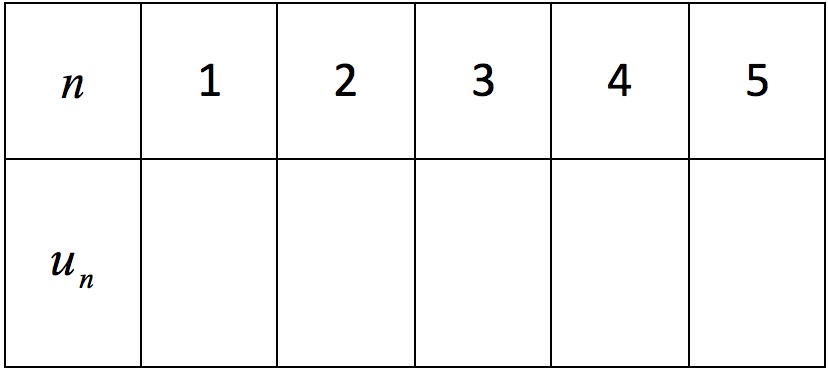

Correction
On détaille uniquement pour .
Ainsi :
Donc :
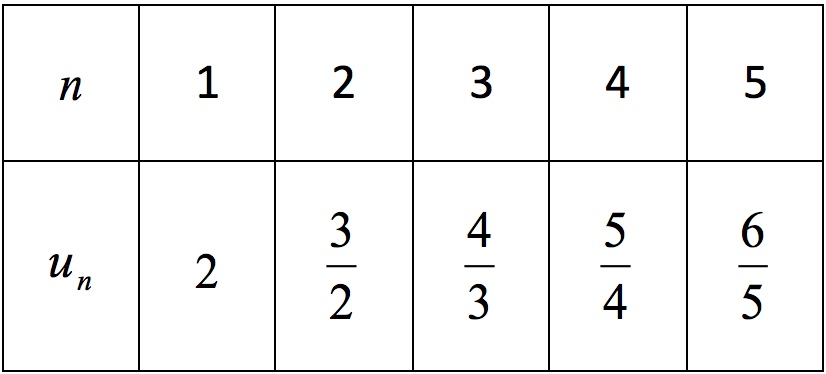
Ainsi :
Donc :

Question 4
Quelle conjecture peut-on faire sur l'expression de en fonction de ?
Démontrer, par récurrence cette conjecture.
Démontrer, par récurrence cette conjecture.
Correction
On conjecture que pour tout entier naturel non nul que .
Démontrons cette conjecture à l'aide d'un raisonnement par récurrence.
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que ainsi .
La propriété est vraie
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
Or :
C'est-à-dire : et car on sait que
On multiplie donc le membre de gauche par : et le membre de droite par :
Maintenant le membre de gauche est égale à :
Après simplification on a :
, il vient alors que la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel non nul, on a vraie, c'est à dire que pour tout entier naturel non nul , on a bien
Démontrons cette conjecture à l'aide d'un raisonnement par récurrence.
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que ainsi .
La propriété est vraie
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
Or :
C'est-à-dire : et car on sait que
On multiplie donc le membre de gauche par : et le membre de droite par :
Maintenant le membre de gauche est égale à :
Après simplification on a :
, il vient alors que la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel non nul, on a vraie, c'est à dire que pour tout entier naturel non nul , on a bien
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.