Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité Session Amérique du Nord mai 2021 Exercice 2 - Exercice 1
35 min
55
Un biologiste s’intéresse à l’évolution de la population d’une espèce animale sur une île du Pacifique.
Au début de l’année , cette population comptait 600 individus. On considère que l’espèce sera menacée d’extinction sur cette île si sa population devient inférieure ou égale à individus.
Le biologiste modélise le nombre d’individus par la suite définie par :
où pour tout entier naturel , désigne le nombre d’individus, en milliers, au début de l’année .
Au début de l’année , cette population comptait 600 individus. On considère que l’espèce sera menacée d’extinction sur cette île si sa population devient inférieure ou égale à individus.
Le biologiste modélise le nombre d’individus par la suite définie par :
où pour tout entier naturel , désigne le nombre d’individus, en milliers, au début de l’année .
Question 1
Estimer, selon ce modèle, le nombre d’individus présents sur l’île au début de l’année puis au début de l’année .
Correction
désigne le nombre d’individus, en milliers, au début de l’année .
D'où :
Il y a individus présents sur l’île au début de l’année .
désigne le nombre d’individus, en milliers, au début de l’année .
D'où :
Il y a individus présents sur l’île au début de l’année .
Question 2
Soit la fonction définie sur l’intervalle par
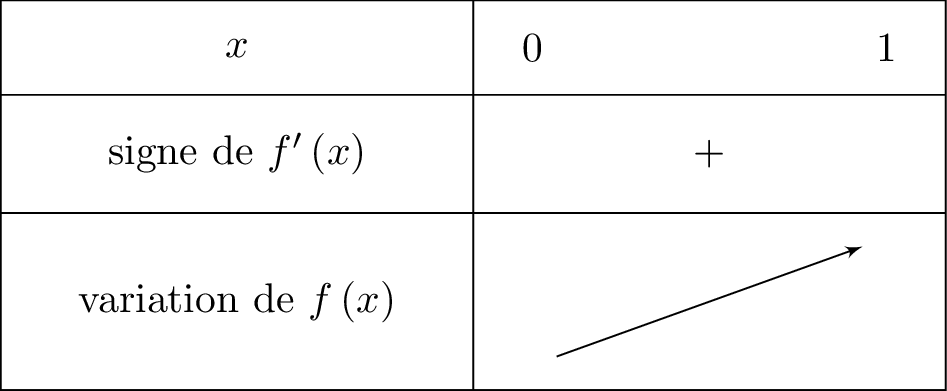
Montrer que la fonction est croissante sur l’intervalle et dresser son tableau de variations.
Correction
Soit
Soit . On commence par développer l'expression de . Ainsi :
Nous allons maintenant calculer la dérivée de .
est dérivable sur .
Ainsi :
De plus :
Il en résulte donc que :
Soit . On commence par développer l'expression de . Ainsi :
Nous allons maintenant calculer la dérivée de .
est dérivable sur .
Ainsi :
De plus :
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.

Question 3
Résoudre dans l’intervalle l’équation .
Correction
Soit
équivaut successivement à :
ou
résolvons qui est déjà résolu :) . résolvons qui donne . D'où : Or et
La solution de l'équation dans l'intervalle est alors :
équivaut successivement à :
ou
La solution de l'équation dans l'intervalle est alors :
Question 4
On remarquera pour la suite de l’exercice que, pour tout entier naturel , .
Démontrer par récurrence que pour tout entier naturel , .
Correction
Pour tout entier naturel , posons la propriété
On a vu précédemment que et .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel ,
On a vu précédemment que et .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel ,
Question 5
En déduire que la suite est convergente.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
Comme cela signifie donc que . La suite est décroissante .
De plus, la suite est minorée par car : .
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 6
Déterminer la limite de la suite .
Correction
Comme la suite est convergente alors elle admet une limite que l'on note .
La suite est donc convergente et définie par .
La fonction est continue sur .
D'après le théorème du point fixe, est solution de l'équation
D'après la question , nous savons que est l’unique réel vérifiant : avec .
La suite est donc convergente et définie par .
La fonction est continue sur .
D'après le théorème du point fixe, est solution de l'équation
D'après la question , nous savons que est l’unique réel vérifiant : avec .
Question 7
Le biologiste a l’intuition que l’espèce sera tôt ou tard menacée d’extinction .
Justifier que, selon ce modèle, le biologiste a raison.
Correction
désigne le nombre d’individus, en milliers, au début de l’année .
D'après la question , nous savons que :
Le nombre d'individus décroit et ce nombre d'individus tend vers .
L'intuition du biologiste s'avère donc vraie.
D'après la question , nous savons que :
Le nombre d'individus décroit et ce nombre d'individus tend vers .
L'intuition du biologiste s'avère donc vraie.
Question 8
def menace()
While
Afficher
While
Afficher
Le biologiste a programmé en langage Python la fonction menace ci-dessus.
Donner la valeur numérique renvoyée lorsqu’on appelle la fonction menace.
Interpréter ce résultat dans le contexte de l’exercice.
Donner la valeur numérique renvoyée lorsqu’on appelle la fonction menace.
Interpréter ce résultat dans le contexte de l’exercice.
Correction
L’algorithme calcule les termes de la suite et l'algorithme s'arrêtera lorsque la valeur du terme recherché sera inférieur à .
Il s’arrête à car et
L’espèce sera donc menacée d’extinction en
Il s’arrête à car et
L’espèce sera donc menacée d’extinction en
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.