Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité Nouvelle-Calédonie 28 août 2023 Jour 1 - Exercice 1
45 min
70
On considère la suite définie par et, pour tout entier naturel , par : .
Question 1
Démontrer que .
Correction
Pour tout entier naturel , nous avons :
Ainsi :
D'où :
Ainsi :
D'où :
Question 2
Déterminer en détaillant le calcul.
Correction
Pour tout entier naturel , nous avons :
Ainsi :
D'où :
Ainsi :
D'où :
Question 3
À l’aide de la calculatrice, conjecturer le sens de variation ainsi que la limite de la suite .
Correction
D'après la calculatrice, on obtient les valeurs des termes de suite d'indice à .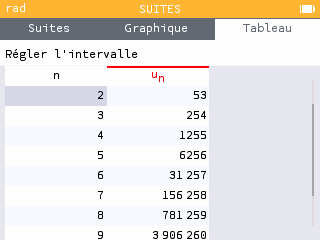 On peut conjecturer que la suite est croissante et sa limite tend vers .
On peut conjecturer que la suite est croissante et sa limite tend vers .

Question 4
Démontrer par récurrence que, pour tout entier naturel , on a : .
Correction
Pour tout entier naturel , posons la propriété
On sait que ainsi .
La propriété est vraie
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire que l'on écrit
Par hypothèse de récurrence :
, on multiplie de part et d'autre de l'inégalité par
, on rajoute (notre objectif est de faire apparaitre dans le membre de gauche )
Ainsi : , il vient alors que la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien
On sait que ainsi .
La propriété est vraie
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire que l'on écrit
Par hypothèse de récurrence :
, on multiplie de part et d'autre de l'inégalité par
, on rajoute (notre objectif est de faire apparaitre dans le membre de gauche )
Ainsi : , il vient alors que la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien
Question 5
En déduire la limite de la suite .
Correction
D'après la question précédente, nous avons montré que pour tout entier naturel , nous avions : .
Comme et alors d'après
Comme et alors d'après
Question 6
On considère la suite définie pour tout entier naturel par : .
Démontrer que la suite est géométrique. Donner sa raison et son premier terme .
Correction
On considère la suite définie pour tout entier naturel par : .
Il vient alors que :
Ainsi :
Ainsi la suite est géométrique de raison et de premier terme c'est à dire .
Il vient alors que :
Ainsi :
Ainsi la suite est géométrique de raison et de premier terme c'est à dire .
Question 7
En déduire, pour tout entier naturel , l’expression de en fonction de .
Correction
- L'expression de en fonction de est donnée par la formule
Question 8
En déduire que pour tout entier naturel : .
Correction
On sait que donc
Il vient alors que :
Il vient alors que :
Question 9
En déduire le sens de variation de la suite .
Correction
Pour tout entier naturel , on a et .
ll en résulte que et de ce fait .
On peut en conclure que la suite est donc croissante.
Question 10
def seuil()
While
return
While
return
On considère la fonction ci-dessus, écrite de manière incomplète en langage Python et destinée à renvoyer le plus petit entier naturel tel que .
Recopier le programme et compléter les deux instructions manquantes.
Recopier le programme et compléter les deux instructions manquantes.
Correction
def seuil()
While
return
While
return
Question 11
Quelle est la valeur renvoyée par cette fonction ?
Correction
La valeur renvoyée par cette fonction est . En effet, il s'agit du rang à partir duquel .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.