Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Montrer que deux plans sont parallèles - Exercice 1
10 min
15
Question 1
Dans l'espace muni d'un repère , on considère les deux plans et admettant pour équation cartésienne
et
et
et sont-ils parallèles ?
Correction
- Soient et des vecteurs normaux respectifs des plans et .
- si et sont colinéaires alors et sont parallèles.
- si et ne sont pas colinéaires alors et ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
On vérifie facilement que les deux vecteurs normaux ne sont pas colinéaires (non proportionnels), alors les plans et ne sont pas parallèles.
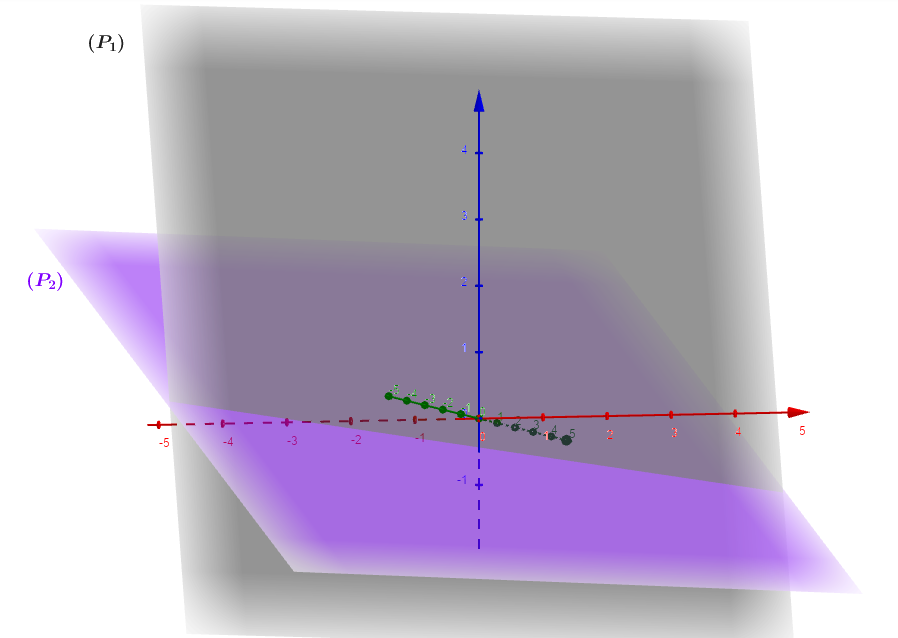
Question 2
Dans l'espace muni d'un repère , on considère les deux plans et admettant pour équation cartésienne
et
et
et sont-ils parallèles ?
Correction
- Soient et des vecteurs normaux respectifs des plans et .
- si et sont colinéaires alors et sont parallèles.
- si et ne sont pas colinéaires alors et ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
, alors les plans et sont parallèles.
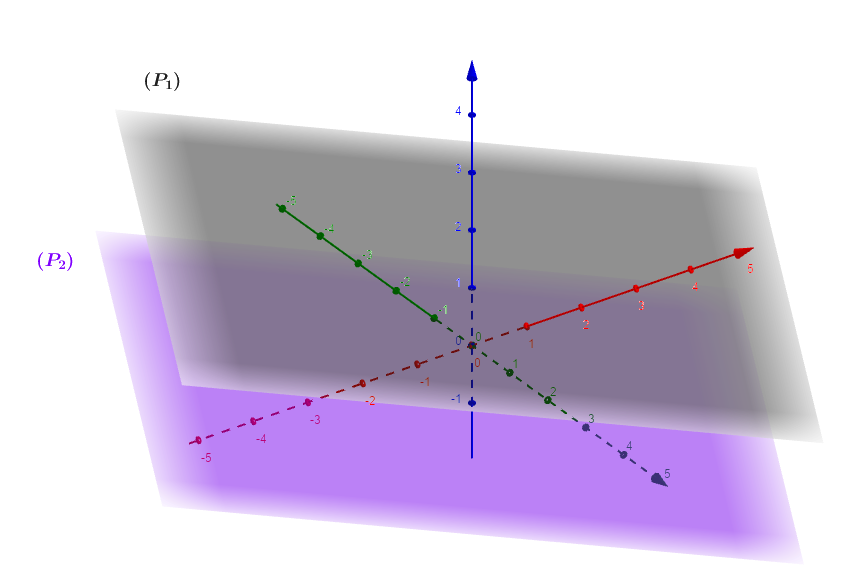
Question 3
Dans l'espace muni d'un repère , on considère les deux plans et admettant pour équation cartésienne
et .
et .
et sont-ils parallèles ?
Correction
- Soient et des vecteurs normaux respectifs des plans et .
- si et sont colinéaires alors et sont parallèles.
- si et ne sont pas colinéaires alors et ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
On vérifie facilement que les deux vecteurs normaux ne sont pas colinéaires (non proportionnels), alors les plans et ne sont pas parallèles.
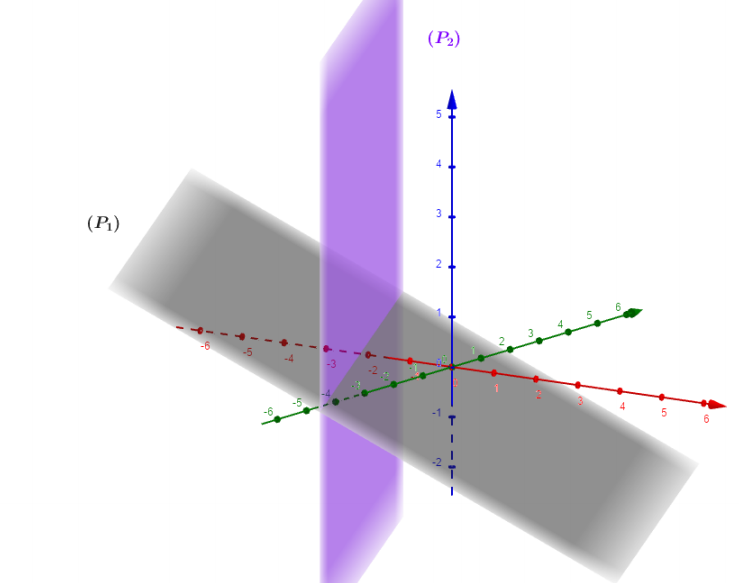
Question 4
Dans l'espace muni d'un repère , on considère les deux plans et admettant pour équation cartésienne
et
et
et sont-ils parallèles ?
Correction
- Soient et des vecteurs normaux respectifs des plans et .
- si et sont colinéaires alors et sont parallèles.
- si et ne sont pas colinéaires alors et ne sont pas parallèles. Cela signifie donc que les plans sont sécants.
On vérifie facilement que les deux vecteurs normaux sont colinéaires car :
, alors les plans et sont parallèles.
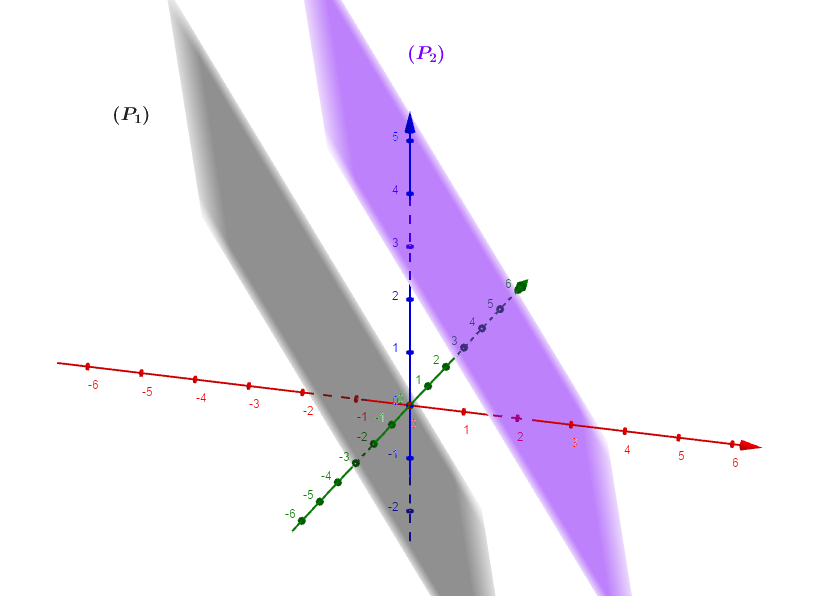
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.