Plan, produit scalaire, orthogonalité et distance dans l'espace
Epreuve d'enseignement de spécialité Session 15 Mars 2021 sujet 2 Exercice 3 : Géométrie dans l'espace - Exercice 1
20 min
40
Dans l'espace muni d'un repère , on considère les points , et
Question 1
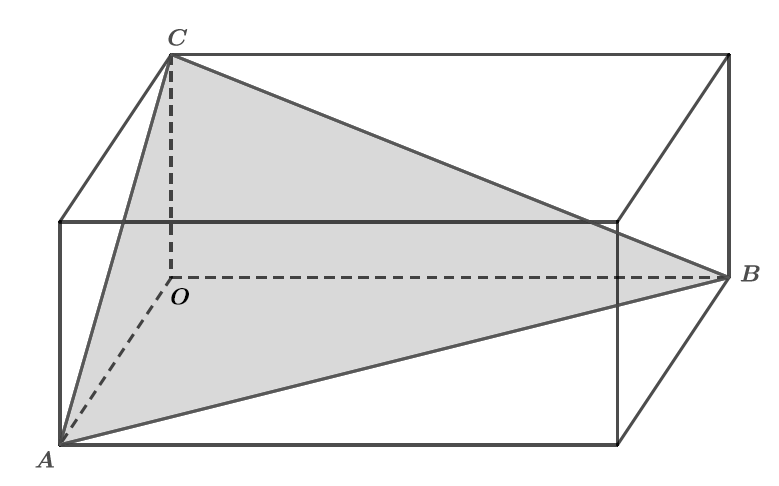
Montrer que le vecteur est normal au plan .
Correction
Un vecteur est normal à un plan s'il est orthogonal à deux vecteurs non colinéaires de .
Nous allons commencer par calculer les vecteurs et .Les vecteurs et sont deux vecteurs non colinéaires du plan .
De plus :
Il en résulte donc que le vecteur est bien orthogonal aux vecteurs non colinéaires et .
On peut alors conclure le vecteur est normal au plan .
Question 2
En déduire qu’une équation cartésienne du plan est : .
Correction
L'écriture cartésienne d'un plan ayant un vecteur normal s'écrit .
Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
D'après la question précédente, le vecteur est normal au plan .Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
Le plan s'écrit .
Or : appartient au plan donc
Ainsi : , d'où
On en conclut que l'équation cartésienne du plan recherché est :
Question 3
On note la droite passant par et orthogonale au plan .
Déterminer une représentation paramétrique de la droite .
Correction
La droite étant orthogonale au plan alors le vecteur normal au plan est un vecteur directeur de la droite .
La droite admet donc le vecteur directeur et passe par le point .
Une représentation paramétrique de la droite est alors :
où
Ainsi :
La droite admet donc le vecteur directeur et passe par le point .
- Soit une droite définie par un point et un vecteur directeur .
La droite admet donc un système d’équations paramétriques, appelé représentation paramétrique, de la forme : où
où
Ainsi :
où
Question 4
Montrer que la droite coupe le plan au point de coordonnées .
Correction
Il faut résoudre le système constitué de l'écriture paramétrique de la droite et du plan pour déterminer la valeur de .
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
où
On remplace la valeur de et dans le plan
où équivaut successivement à
où
où
où
Maintenant que nous avons la valeur de , on peut obtenir les valeurs de et
Il en résulte que
Les coordonnées du point d'intersection entre la droite et le plan est bien le point
Question 5
Calculer la distance .
Correction
Soit un repère orthonormal de l'espace et deux points et . La distance est donnée par la formule :
Nous savons que et Il vient alors que :
D'où :
Question 6
On rappelle que le volume d’une pyramide est donné par : où est l’aire d’une base et est la hauteur de la pyramide correspondant à cette base.
En calculant de deux façons différentes le volume de la pyramide , déterminer l’aire du triangle .
Correction
Nous allons calculer l'aire de la pyramide de deux manières différentes.
Nous savons que le volume d’une pyramide est donné par : où est l’aire d’une base et est la hauteur de la pyramide correspondant à cette base.
Dans cette première situation, nous allons prendre comme aire de la base le triangle rectangle en et la hauteur le segment .
Dans l'espace muni d'un repère , on considère les points , et
Ainsi, la distance et la distance .
D'où :
or
Ainsi :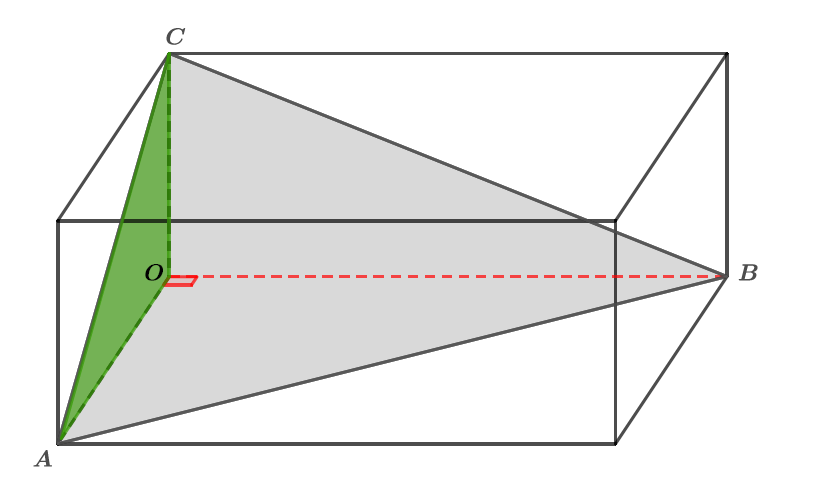
Nous savons que le volume d’une pyramide est donné par : où est l’aire d’une base et est la hauteur de la pyramide correspondant à cette base.
Dans cette deuxième situation, nous allons prendre comme aire de la base le triangle rectangle en et la hauteur le segment .
Dans l'espace muni d'un repère , on considère les points , et
Ainsi, la distance et la distance .
D'où :
or
Ainsi :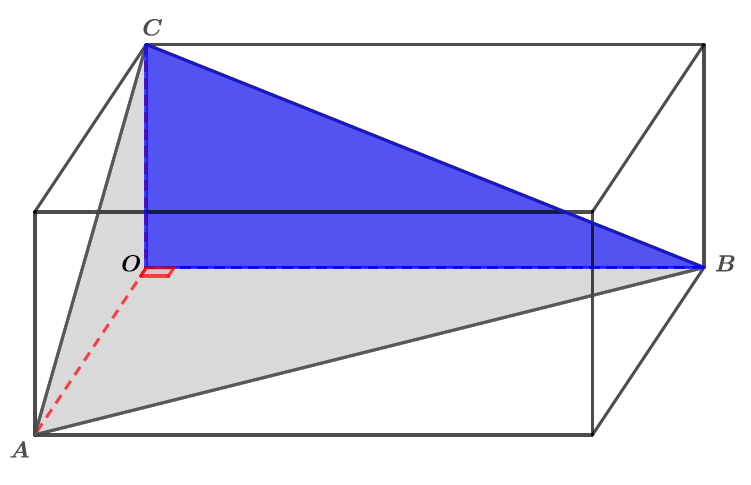
Nous savons que le volume d’une pyramide est donné par : où est l’aire d’une base et est la hauteur de la pyramide correspondant à cette base.
Dans cette première situation, nous allons prendre comme aire de la base le triangle rectangle en et la hauteur le segment .
Dans l'espace muni d'un repère , on considère les points , et
Ainsi, la distance et la distance .
D'où :
or
Ainsi :
unité de volume

Nous savons que le volume d’une pyramide est donné par : où est l’aire d’une base et est la hauteur de la pyramide correspondant à cette base.
Dans cette deuxième situation, nous allons prendre comme aire de la base le triangle rectangle en et la hauteur le segment .
Dans l'espace muni d'un repère , on considère les points , et
Ainsi, la distance et la distance .
D'où :
or
Ainsi :
unité de volume
