Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité Métropole 13 Septembre 2021 J1 Exercice A : Géométrie dans l'espace - Exercice 1
35 min
55
On considère le cube ABCDEFGH donné ci-dessous.
On donne trois points , et vérifiant :
, et
Les points , et sont représentés sur la figure. On se place dans le repère orthonormé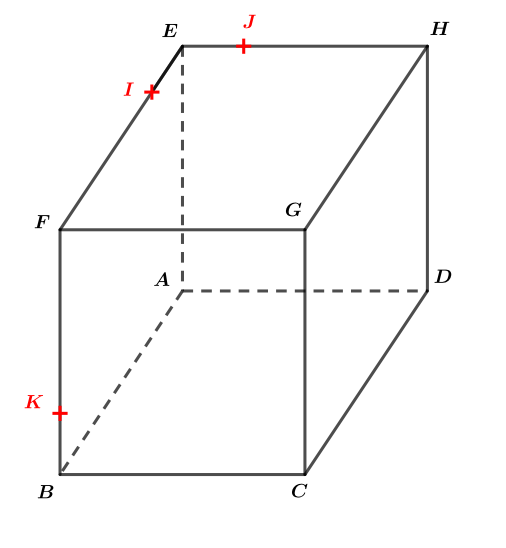
On donne trois points , et vérifiant :
, et
Les points , et sont représentés sur la figure. On se place dans le repère orthonormé

Question 1
Donner les coordonnées des points , et .
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
est l'origine du repère ainsi .
Ainsi :
Ainsi :
Ainsi :
Question 2
Démontrer que le vecteur est normal au plan .
Correction
Un vecteur est normal à un plan s'il est orthogonal à deux vecteurs non colinéaires de .
Nous allons commencer par calculer les vecteurs et .Les vecteurs et sont deux vecteurs non colinéaires du plan .
De plus , nous allons calculer le vecteur .On lit facilement, sur le cube, les coordonnées des points et qui sont et .
Ce qui nous donne :
Finalement :
Il en résulte donc que le vecteur est bien orthogonal aux vecteurs non colinéaires et .
On peut alors conclure le vecteur est normal au plan .
Question 3
Montrer qu’une équation cartésienne du plan est
Correction
L'écriture cartésienne d'un plan ayant un vecteur normal s'écrit .
Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
D'après la question précédente, le vecteur est normal au plan .Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
Le plan s'écrit .
Or : appartient au plan donc
Ainsi : , d'où
On en conclut que l'équation cartésienne du plan recherché est :
Nous pouvons multiplier tous les coefficients de l'équation cartésienne par .
Il en résulte donc qu’une équation cartésienne du plan est bien :
Question 4
Déterminer une représentation paramétrique de la droite .
Correction
Les coordonnés des points et sont respectivement et .
On commence par calculer le vecteur
Soit le point appartenant à la droite .
Cela donne :
puis
Les points , et sont alignés, donc les vecteurs et sont colinéaires.
Cela se traduit par :
, ce qui donne où
Finalement l'équation paramétrique de est :
On commence par calculer le vecteur
- On commence par calculer le vecteur qui est un vecteur directeur de la droite .
Ensuite soit un point de cordonnées qui appartient à la droite .
Cela signifie que les points et sont alignés donc les vecteurs et sont colinéaires.
Il existe alors un réel tel que . On aura ainsi la droite .
Cela donne :
puis
Les points , et sont alignés, donc les vecteurs et sont colinéaires.
Cela se traduit par :
, ce qui donne où
Finalement l'équation paramétrique de est :
où
Question 5
En déduire les coordonnées du point , point d’intersection de la droite avec le plan .
Correction
D'après les question précédentes, nous savons que :
L'équation paramétrique de la droite est : où
L'équation cartésienne du plan est :
Les coordonnées du point , point d’intersection de la droite avec le plan doivent vérifier le système suivant :
On remplace la valeur de et dans le plan
Maintenant que nous avons la valeur de , on peut obtenir les valeurs de et
Les coordonnées du point , point d’intersection de la droite avec le plan sont alors
L'équation paramétrique de la droite est : où
L'équation cartésienne du plan est :
Les coordonnées du point , point d’intersection de la droite avec le plan doivent vérifier le système suivant :
On remplace la valeur de et dans le plan
Maintenant que nous avons la valeur de , on peut obtenir les valeurs de et
Les coordonnées du point , point d’intersection de la droite avec le plan sont alors
Question 6
Sur la figure en annexe, placer le point et construire l’intersection du plan avec la face .
Correction
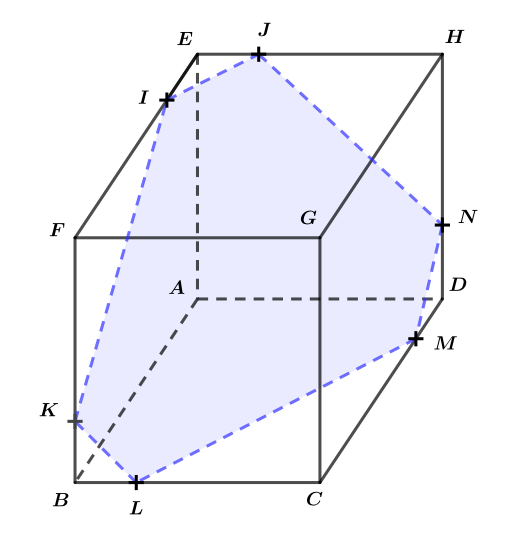
Question 7
Soit . Montrer que les points , , et sont coplanaires.
Correction
D'après la question , on a montré que le point appartient au plan . Cela signifie que les points et sont coplanaires.
Vérifions maintenant si le point appartient également au plan :
Il vient alors que :
Le point appartient également au plan .
Il en résulte donc que les points et appartiennent bien au plan .
On peut alors conclure que les points , , , et sont alors coplanaires car ils sont tous dans le même plan.
Finalement, les points , , et sont alors coplanaires.
Vérifions maintenant si le point appartient également au plan :
Il vient alors que :
Le point appartient également au plan .
Il en résulte donc que les points et appartiennent bien au plan .
On peut alors conclure que les points , , , et sont alors coplanaires car ils sont tous dans le même plan.
Finalement, les points , , et sont alors coplanaires.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.