Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité Amérique du Sud 27 septembre 2022 Sujet 2 - Exercice 1
30 min
50
L'espace est muni d'un repère , on considère les points , et 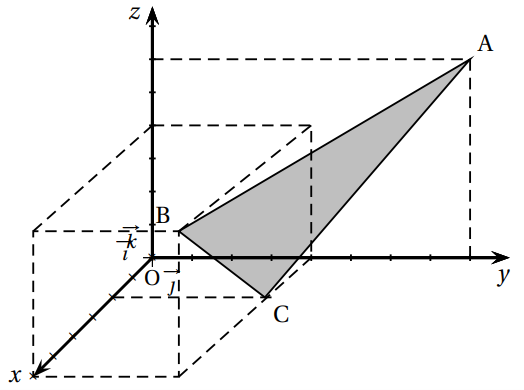

Question 1
Justifier que les points et ne sont pas alignés .
Correction
On vérifie facilement que les deux vecteurs ne sont pas colinéaires, alors les points et ne sont pas alignés donc ils définissent un plan.
Question 2
Montrer que le vecteur est un vecteur normal au plan .
Correction
Calculons et
D'une part :
D'autre part :
est orthogonal à deux vecteurs et non colinéaires du plan .
Il en résulte donc que le vecteur est un vecteur normal au plan .
D'une part :
D'autre part :
est orthogonal à deux vecteurs et non colinéaires du plan .
Il en résulte donc que le vecteur est un vecteur normal au plan .
Question 3
Déterminer une équation cartésienne du plan .
Correction
L'écriture cartésienne d'un plan ayant un vecteur normal s'écrit .
Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
le vecteur est un vecteur normal au plan .Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
Ici le plan s'écrit
Or : appartient au plan donc
Ainsi : , d'où
On en conclut que l'équation cartésienne du plan recherché est :
Question 4
Soient et les points de coordonnées respectives et .
Déterminer une représentation paramétrique de la droite .
Déterminer une représentation paramétrique de la droite .
Correction
Les coordonnés des points et les points de coordonnées respectives et .
On commence par calculer le vecteur
Soit le point appartenant à la droite .
Cela donne :
puis
Les points , et sont alignés, donc les vecteurs et sont colinéaires.
Cela se traduit par :
, ce qui donne où
Finalement l'équation paramétrique de est :
On commence par calculer le vecteur
- On commence par calculer le vecteur qui est un vecteur directeur de la droite .
Ensuite soit un point de cordonnées qui appartient à la droite .
Cela signifie que les points et sont alignés donc les vecteurs et sont colinéaires.
Il existe alors un réel tel que . On aura ainsi la droite .
Cela donne :
puis
Les points , et sont alignés, donc les vecteurs et sont colinéaires.
Cela se traduit par :
, ce qui donne où
Finalement l'équation paramétrique de est :
où
Question 5
Montrer que le milieu du segment appartient à la droite .
Correction
est le milieu du segment .
Ainsi : on obtient alors .
On remplace les coordonnées de dans l'équation de la droite
Donc ce qui donne
Puis on résout les équations et on doit pour chaque ligne trouver la même valeur de pour que le point appartienne à .
Finalement, le milieu du segment appartient bien à la droite .
Ainsi : on obtient alors .
On remplace les coordonnées de dans l'équation de la droite
Donc ce qui donne
Puis on résout les équations et on doit pour chaque ligne trouver la même valeur de pour que le point appartienne à .
Finalement, le milieu du segment appartient bien à la droite .
Question 6
On considère le triangle . Déterminer la nature du triangle .
Correction
Nous savons que et d'après la question .
Or :
Le triangle est isocèle en .
Or :
Le triangle est isocèle en .
Question 7
Calculer l’aire du triangle en unité d’aire.
Correction
est le milieu de la base du triangle isocèle, donc est une médiane du triangle.
Or dans un triangle isocèle, une médiane est également une hauteur du triangle.
Son aire est donc égale à :
Il nous faut donc calculer les distances et .
Il vient alors que :
Finalement :
Or dans un triangle isocèle, une médiane est également une hauteur du triangle.
Son aire est donc égale à :
Il nous faut donc calculer les distances et .
Il vient alors que :
Finalement :
unités d’aire.
Question 8
Calculer .
Correction
Nous savons que et d'après la question .
Or :
Or :
Question 9
En déduire une mesure de l’angle arrondie à degré.
Correction
D'après les questions précédentes, ,nous savons que :
; et .
Pour déterminer la mesure de l'angle , nous allons utiliser la formule du produit scalaire utilisant le cosinus.
Ainsi :
; et .
Pour déterminer la mesure de l'angle , nous allons utiliser la formule du produit scalaire utilisant le cosinus.
- Le produit scalaire de deux vecteurs et non nuls est défini par :
Ainsi :
°
Question 10
On considère le point de coordonnées .
Montrer que est le projeté orthogonal du point sur le plan . En déduire la distance du point au plan .
Montrer que est le projeté orthogonal du point sur le plan . En déduire la distance du point au plan .
Correction
On vérifie dans un premier temps que le point appartient au plan .
En effet : . De plus :
Dans un second temps, on vérifie que :
est orthogonal à deux vecteurs et non colinéaires du plan .
Il en résulte donc que le vecteur est un vecteur normal au plan .
Comme le point appartient au plan , il en résulte donc que est le projeté orthogonal du point sur le plan .
Finalement, la distance du point au plan correspond tout simplement à la distance .
En effet : . De plus :
Dans un second temps, on vérifie que :
est orthogonal à deux vecteurs et non colinéaires du plan .
Il en résulte donc que le vecteur est un vecteur normal au plan .
Comme le point appartient au plan , il en résulte donc que est le projeté orthogonal du point sur le plan .
Finalement, la distance du point au plan correspond tout simplement à la distance .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.