Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Calculer un produit scalaire de deux vecteurs dans l'espace - Exercice 3

10 min
25
Soit ABCDEFGHABCDEFGH un cube d'arête 88 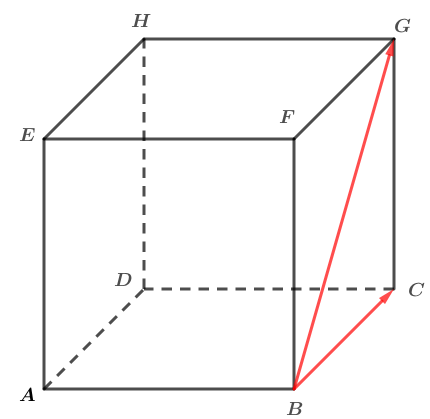cm .
Question 1

Calculer BC→⋅BG→\overrightarrow{BC} \cdot \overrightarrow{BG}

Correction
La face BCGFBCGF du cube est un carré.
Soit CC le projeté orthogonal de GG sur le segment [BC]\left[BC\right] . Il en résulte donc que :
BC→⋅BG→=BC→⋅BC→\overrightarrow{BC} \cdot \overrightarrow{BG}=\overrightarrow{BC} \cdot \overrightarrow{BC}
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs BC→\overrightarrow{BC} et BC→\overrightarrow{BC} sont colinéaires et de même sens.
Il vient alors que :
BC→⋅BG→=BC×BC\overrightarrow{BC} \cdot \overrightarrow{BG}=BC \times BC
BC→⋅BG→=8×8\overrightarrow{BC} \cdot \overrightarrow{BG}=8 \times 8
Ainsi :
BC→⋅BG→=64\overrightarrow{BC} \cdot \overrightarrow{BG}=64
Question 2
Soit ABCDABCD un tétraèdre. Les unités des mesures sont en centimètres.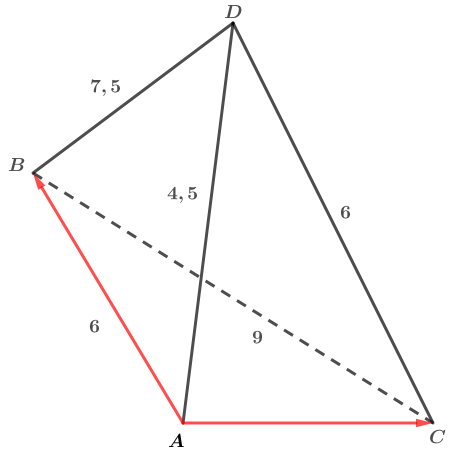
On note que AC=5AC=5 cm

Calculer AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
    Soit ABCABC un triangle dont l'on connait les mesures des 33 côtés.
  • On a : AB→⋅AC→=12[AB2+AC2−CB2]\overrightarrow{AB} \cdot \overrightarrow{AC} =\frac{1}{2} \left[AB^{2} +AC^{2} -CB^{2} \right]
D'après le rappel, nous savons que :
AB→⋅AC→=12[AB2+AC2−CB2]\overrightarrow{AB} \cdot \overrightarrow{AC} =\frac{1}{2} \left[AB^{2} +AC^{2} -CB^{2} \right] . Il ne nous reste plus qu'à substituer par les valeurs des côtés que l'on connait :
AB→⋅AC→=12[62+52−92]\overrightarrow{AB} \cdot \overrightarrow{AC} =\frac{1}{2} \left[6^{2} +5^{2} -9^{2} \right]
AB→⋅AC→=12[36+25−81]\overrightarrow{AB} \cdot \overrightarrow{AC} =\frac{1}{2} \left[36 +25 -81 \right]
AB→⋅AC→=12×(−20)\overrightarrow{AB} \cdot \overrightarrow{AC} =\frac{1}{2} \times \left(-20\right)
AB→⋅AC→=−10\overrightarrow{AB} \cdot \overrightarrow{AC} =-10
Question 3
Soit ABCDEFGHABCDEFGH un cube d'arête 88 cm .

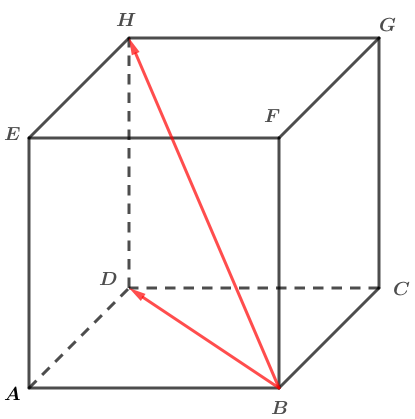
Calculer BD→⋅BH→\overrightarrow{BD} \cdot \overrightarrow{BH}

Correction
ABCDEFGHABCDEFGH un cube d'arête 88 cm . Il en résulte que le triangle BDHBDH est rectangle en DD.
Soit DD le projeté orthogonal de HH sur le segment [DB]\left[DB\right] . Il en résulte donc que :
BD→⋅BH→=BD→⋅BD→\overrightarrow{BD} \cdot \overrightarrow{BH}=\overrightarrow{BD} \cdot \overrightarrow{BD}
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs BD→\overrightarrow{BD} et BD→\overrightarrow{BD} sont colinéaires et de même sens.
Il vient alors que :
BD→⋅BH→=BD×BD\overrightarrow{BD} \cdot \overrightarrow{BH}=BD \times BD
BD→⋅BH→=BD2\overrightarrow{BD} \cdot \overrightarrow{BH}=BD^{2}
Il nous faut maintenant déterminer la mesure du segment [BD]\left[BD\right]. Nous savons que le triangle DABDAB est rectangle en AA.
Nous allons utiliser le théorème de Pythagore :
DB2=AD2+AB2DB^{2} =AD^{2} +AB^{2}
DB2=82+82DB^{2} =8^{2} +8^{2}
DB2=64+64DB^{2} =64+64
DB2=128DB^{2} =128
DB=128DB=\sqrt{128}
Nous pouvons maintenant calculer BD→⋅BH→=BD2\overrightarrow{BD} \cdot \overrightarrow{BH}=BD^{2}
Ce qui nous donne :
BD→⋅BH→=(128)2\overrightarrow{BD} \cdot \overrightarrow{BH}=\left(\sqrt{128}\right)^{2}
Ainsi :
BD→⋅BH→=128\overrightarrow{BD} \cdot \overrightarrow{BH}=128

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.