Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 3
40 min
65
On considère l’équation différentielle .
Question 1
Démontrer que la fonction définie sur l’ensemble des nombres réels par est une solution de .
Correction
Dans un premier temps, nous allons calculer la dérivée de la fonction .
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
Maintenant, est une solution de si et seulement si .
Il vient alors que :
Finalement :
Donc est bien une solution de l’équation différentielle
est dérivable sur .
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
Maintenant, est une solution de si et seulement si .
Il vient alors que :
Finalement :
Donc est bien une solution de l’équation différentielle
Question 2
Résoudre l’équation différentielle .
Correction
Soit l’équation différentielle où est un réel avec , et où est une fonction de la variable définie et dérivable sur .
Les solutions de cette équation sont les fonctions de la forme : où est une constante réelle.
Nous allons transformer l'écriture afin de revenir à une forme . Ainsi:équivaut successivement à :
On identifie ici que : .
Il en résulte que les solutions de l'équation sont alors : où est une constante réelle.
Finalement :
où est une constante réelle.
Question 3
Démontrer qu’une fonction , définie et dérivable sur est solution de si et seulement si est solution de
Correction
est une solution de si et seulement si .
D'après la question , nous avons montré que .
Comme et que alors nous pouvons écrire que :
Il en résulte donc bien que est une solution de si et seulement si est une solution de .
D'après la question , nous avons montré que .
Comme et que alors nous pouvons écrire que :
Il en résulte donc bien que est une solution de si et seulement si est une solution de .
Question 4
En déduire toutes les solutions de
Correction
D'après la question , nous savons que les solutions de l’équation différentielle sont
D'après la question , nous savons que est solution de si et seulement si est une solution de l’équation différentielle .
Il en résulte donc que :
où est une constante réelle. Nous savons également que :
où est une constante réelle.
Les solutions de l’équation sont alors :
où est une constante réelle.
D'après la question , nous savons que est solution de si et seulement si est une solution de l’équation différentielle .
Il en résulte donc que :
où est une constante réelle. Nous savons également que :
où est une constante réelle.
Les solutions de l’équation sont alors :
où est une constante réelle.
Question 5
Déterminer la fonction solution de qui prend la valeur en
Correction
Soit où est une constante réelle tel que
Il vient alors que :
équivaut successivement à :
Ainsi :
La fonction la fonction solution de qui prend la valeur en est alors :
Il vient alors que :
équivaut successivement à :
Ainsi :
La fonction la fonction solution de qui prend la valeur en est alors :
Question 6
étant un nombre réel donné, on note la fonction définie sur l’ensemble par :
.
On note la courbe représentative de la fonction dans un repère orthonormal
Déterminer les limites de en .
Correction
Commençons par calculer
On commence par calculer .
On pose . Lorsque tend vers alors tend vers .
Or :
Par composition :
Ainsi :
On commence par calculer .
On pose . Lorsque tend vers alors tend vers .
Or :
Par composition :
Ainsi :
Question 7
Déterminer les limites de en
Correction
Pour calculer la limite en , nous allons commencer par développer l'expression de la fonction .
L’axe des abscisses est donc asymptote horizontale à au voisinage de plus l’infini.
L’axe des abscisses est donc asymptote horizontale à au voisinage de plus l’infini.
Question 8
Calculer pour tout réel
Correction
Soit
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
. Nous allons factoriser l'expression par
Ainsi :
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
. Nous allons factoriser l'expression par
Ainsi :
Question 9
En déduire le tableau de variations de
Correction
Pour tout réel , 0
Le signe de est celui de .
Il en résulte donc que :
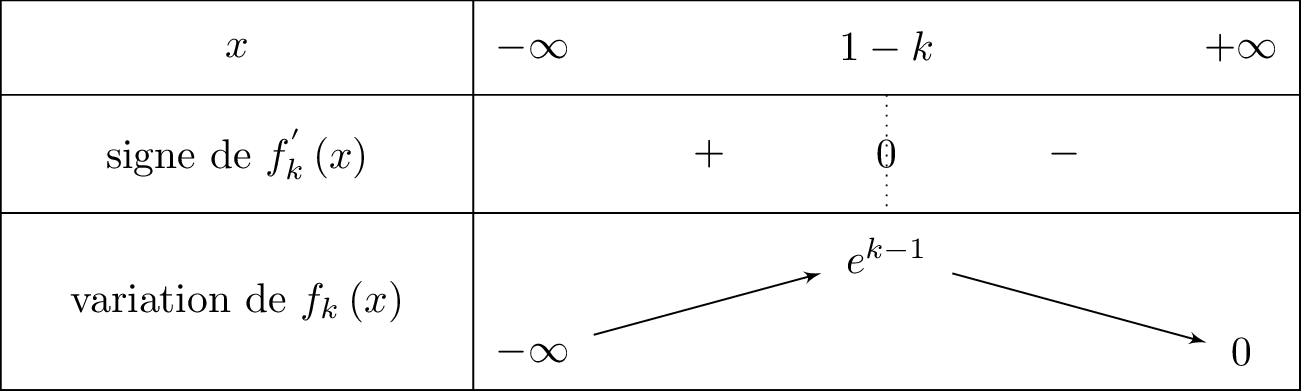 Avec :
Avec :
Le signe de est celui de .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.