Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Variations de dérivées composées - Exercice 1
20 min
35
Dresser le tableau de variation des fonctions suivantes, en donnant dans un premier temps leur domaine de dérivabilité.
Question 1
Correction
La fonction est définie si et seulement si .
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi , on va tout mettre au même dénominateur pour étudier le signe de .
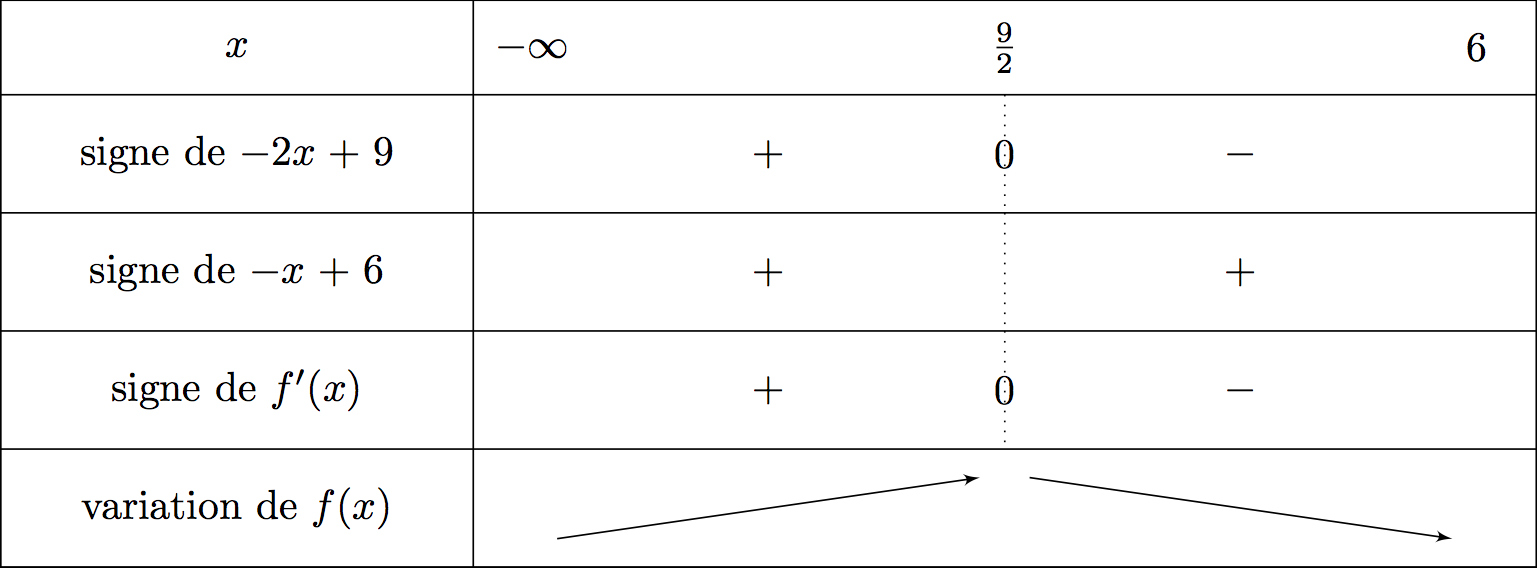
Finalement
Comme alors
On cherche aussi le signe de . Ainsi .
Cela signifie que l'on mettra le signe pour le signe de dès que
On traduit ces informations dans un tableau de variation
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi , on va tout mettre au même dénominateur pour étudier le signe de .
Finalement
Comme alors
On cherche aussi le signe de . Ainsi .
Cela signifie que l'on mettra le signe pour le signe de dès que
On traduit ces informations dans un tableau de variation

Question 2
Correction
Comme pour tout réel , on sait que
La fonction est définie si et seulement si .
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
Comme pour tout réel, on sait que et que , on dresse le tableau de variation, ci-dessous

La fonction est définie si et seulement si .
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
Comme pour tout réel, on sait que et que , on dresse le tableau de variation, ci-dessous

Question 3
Correction
La fonction est définie si et seulement si .
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
Pour tout réel ~on sait que .
Pour étudier le signe de , on utilise le discriminant.
, il n'y a pas de racines réelles. Ainsi .
On résume tout cela dans un tableau de variation

Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
, on va tout mettre au même dénominateur pour étudier le signe de .
Pour tout réel ~on sait que .
Pour étudier le signe de , on utilise le discriminant.
, il n'y a pas de racines réelles. Ainsi .
On résume tout cela dans un tableau de variation

Question 4
Correction
La fonction est définie si et seulement si .
Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
Le numérateur est positif, le signe de est alors du signe du dénominateur .
Comme alors .
On cherche à savoir le signe de , ainsi .
On résume tout cela dans un tableau de variation

Ainsi le domaine de définition est .
De plus le domaine de dérivabilité est le même intervalle que celui du domaine de définition. Ainsi est dérivable sur .
On reconnait la forme
On a et
Ainsi
Le numérateur est positif, le signe de est alors du signe du dénominateur .
Comme alors .
On cherche à savoir le signe de , ainsi .
On résume tout cela dans un tableau de variation

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.