Résoudre une inéquation avec des logarithmes - Exercice 4

$$\blue{\text{Dans un premier temps,}}$$ nous allons chercher les racines de la fonction du second degré suivante : $$x\mapsto-3x^{2}+9x+30$$
On utilise le discriminant .
Il existe donc deux racines réelles distinctes notées $$x_{1}$$ et $$x_{2}$$ tels que $$x_{1} =\frac{-b-\sqrt{\Delta } }{2a}$$ et $$x_{2} =\frac{-b+\sqrt{\Delta } }{2a}$$
$$x_{1} =5$$ et $$x_{2} =-2$$.
Avec un rappel de première, nous allons pouvoir factoriser la fonction $$x\mapsto-3x^{2}+9x+30$$
Il en résulte donc que nous pouvons écrire $$x\mapsto -3\left(x-5 \right)\left(x+2 \right)$$
$$\blue{\text{Dans un deuxième temps}}$$, nous voulons résoudre l'inéquation : $$-3\left(\ln \left(x\right)\right)^{2} +9\ln \left(x\right)+30\ge0$$ . Soit $$x$$ un réel strictement positif.
On commence par un changement de variable. On pose $$X=\ln \left(x\right)$$. Il vient alors que :
$$-3X^{2} +9X+30\ge0$$. Nous sommes en mesure maintenant de factoriser cette expression comme vue au début de la question. Cela nous donne :
$$-3\left(X-5 \right)\left(X+2 \right)\ge0$$ . Or nous avons posé comme changement de variable $$X=\ln \left(x\right)$$.
Ainsi, nous obtenons :
$$-3\left(\ln \left(x\right)-5 \right)\left(\ln \left(x\right)+2 \right)\ge0$$ . Pour résoudre cette inéquation, nous allons dresser un tableau de signe.

$$\red{\text{D'une part :}}$$

$$\ln \left(x\right)-5\ge 0\Leftrightarrow \ln \left(x\right)\ge 5\Leftrightarrow \ln \left(x\right)\ge \ln \left(e^{5} \right)\Leftrightarrow x\ge e^{5}$$
(On commencera dans la ligne $$\ln \left(x\right)-5$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x\ge e^{5}$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)

$$\red{\text{D'autre part :}}$$

$$\ln \left(x\right)+2\ge 0\Leftrightarrow \ln \left(x\right)\ge -2\Leftrightarrow \ln \left(x\right)\ge \ln \left(e^{-2} \right)\Leftrightarrow x\ge e^{-2}$$
(On commencera dans la ligne $$\ln \left(x\right)+2$$ par le signe $$\left(-\right)$$ et dès que l'on dépasse la valeur $$x\ge e^{-2}$$ on mettra le signe $$\left(+\right)$$ dans le tableau de signe.)

$$\red{\text{Enfin :}}$$ $$-3$$ est strictement négatif. On mettra que le signe $$\left(-\right)$$ dans la ligne de $$-3$$.

Le tableau du signe du produit est donné ci-dessous :
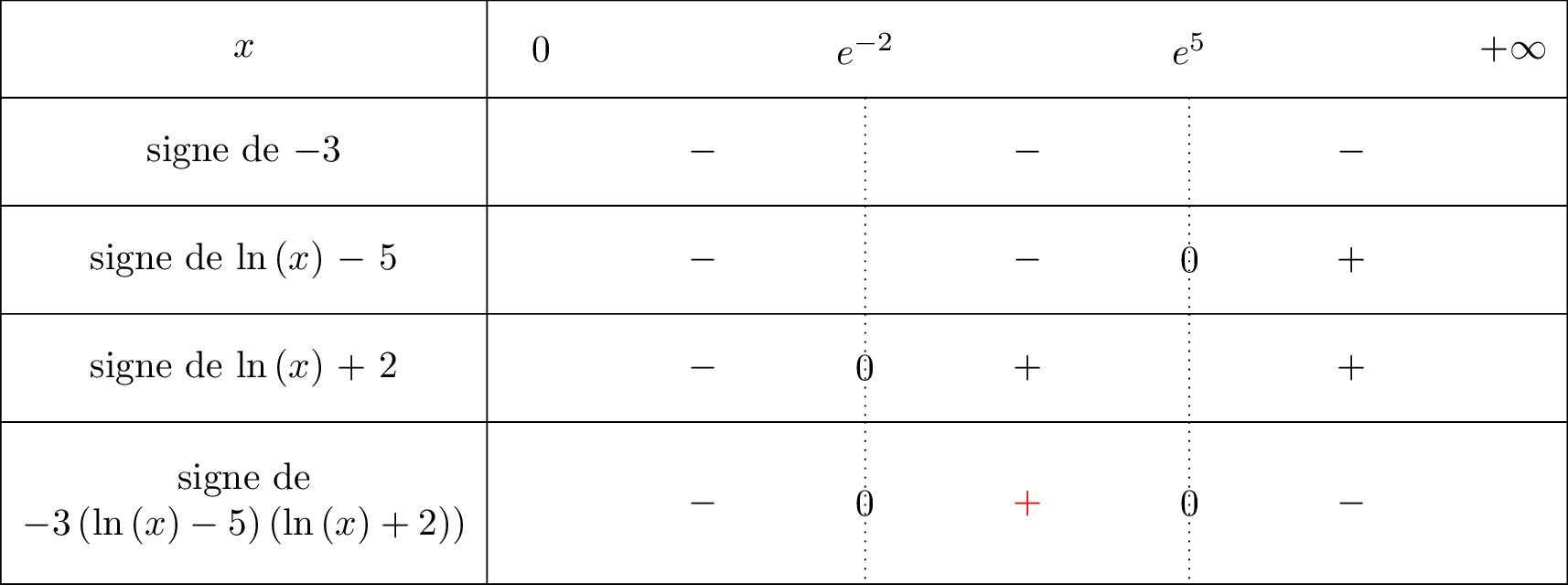Finalement, les solutions de l'inéquation $$-3\left(\ln \left(x\right)\right)^{2} +9\ln \left(x\right)+30\ge0$$ sont les mêmes que les solutions de l'inéquation $$-3\left(\ln \left(x\right)-5 \right)\left(\ln \left(x\right)+2 \right)\ge0$$ .
D'après le tableau de signe, on a alors :