Résoudre une inéquation avec des logarithmes - Exercice 3

$$P\left(-2\right)=2\left(-2\right)^{3} -6\left(-2\right)^{2} -12\left(-2\right)+16$$ équivaut successivement à
$$P\left(-2\right)=-16-24+24+16$$

On va débuter par développer l'expression $$P\left(x\right)=\left(x+2\right)\left(ax^{2} +bx+c\right)$$
$$P\left(x\right)=\left(x+2\right)\left(ax^{2} +bx+c\right)\Leftrightarrow P\left(x\right)=ax^{3} +bx^{2} +cx+2ax^{2} +2bx+2c$$
Ainsi $$P\left(x\right)=ax^{3} +x^{2} \left(b+2a\right)+x\left(c+2b\right)+2c$$
Il faut que :
$$P\left(x\right)={\color{blue}a}x^{3} +x^{2} \left({\color{red}b+2a}\right)+x\left({\color{purple}c+2b}\right)+{\color{darkgreen}2c}$$ soit égal à $$P\left(x\right)={\color{blue}2}x^{3}{\color{red}-6} x^{2} {\color{purple}-12}x+{\color{darkgreen}16}$$.
Deux polynômes sont égaux si et seulement leurs coefficients respectifs sont égaux.
Par identification, on obtient le système suivant
$$\left\{\begin{array}{ccc} {{\color{blue}a}} & {=} & {{\color{blue}2}} \\ {{\color{red}b+2a}} & {=} & {{\color{red}-6}} \\ {{\color{purple}c+2b}} & {=} & {{\color{purple}-12}} \\ {{\color{darkgreen}2c}} & {=} & {{\color{darkgreen}16}} \end{array}\right.$$ Il en résulte que $$\left\{\begin{array}{ccc} {a} & {=} & {2} \\ {b} & {=} & {-10} \\ {b} & {=} & {-10} \\ {c} & {=} & {8} \end{array}\right.$$
Il vient alors que

Il s'agit d'une équation produit nul.
$$P\left(x\right)=0\Leftrightarrow P\left(x\right)=\left(x+2\right)\left(2x^{2} -10x+8\right)=0\Leftrightarrow x+2=0$$ et $$2x^{2} -10x+8=0$$
$$x+2=0\Leftrightarrow x=-2$$
$$2x^{2} -10x+8=0$$ on utilise ici le discriminant $$\Delta =36$$
$$x_{1} =\frac{-b-\sqrt{\Delta } }{2a} =1$$ et $$x_{2} =\frac{-b+\sqrt{\Delta } }{2a} =4$$
Les solutions de l'équation $$P\left(x\right)=0$$ sont alors :

$$P\left(x\right)\ge 0\Leftrightarrow \left(x+2\right)\left(2x^{2} -10x+8\right)\ge 0.$$
On va dresser le tableau de signe de cette inéquation.

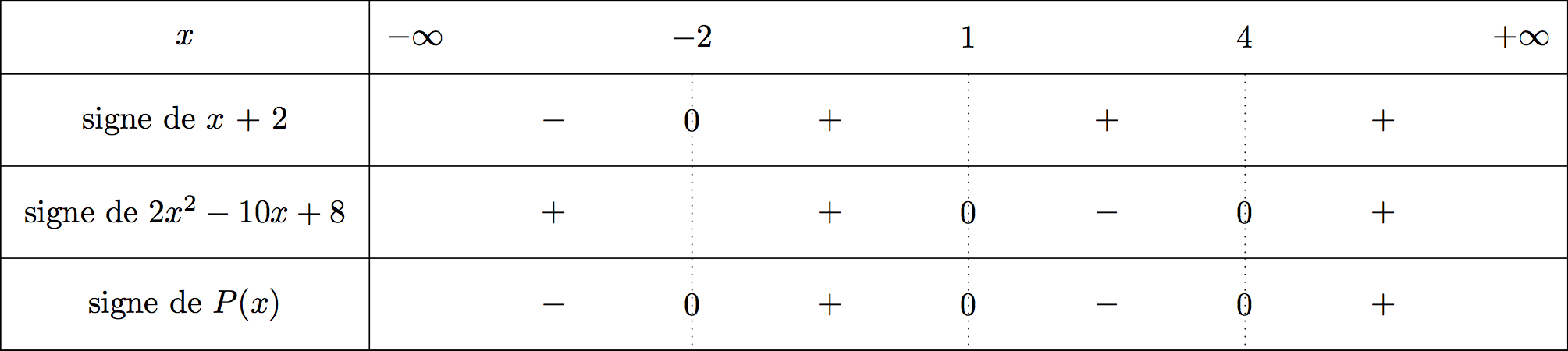
Ainsi :

L'inéquation est définie si et seulement si $$\left\{\begin{array}{c} {x>0} \\ {\text{ et }} \\ {2x-6>0} \\ {\text{ et }} \\ {6x-8>0} \end{array}\right. \Leftrightarrow \left\{\begin{array}{c} {x>0} \\ {\text{ et }} \\ {x>3} \\ {\text{ et }} \\ {x>\frac{4}{3} } \end{array}\right.$$
Ainsi le domaine de définition pour cette inéquation est $$Df=\left]3;+\infty \right[$$
Simplifions puis résolvons cette inéquation.
$$2\ln \left(x\right)+\ln \left(2x-6\right)\ge \ln \left(2\right)+\ln \left(6x-8\right)$$ équivaut successivement à
$$\ln \left(x^{2} \right)+\ln \left(2x-6\right)\ge \ln \left(2\times \left(6x-8\right)\right)$$
$$\ln \left(x^{2} \left(2x-6\right)\right)\ge \ln \left(12x-16\right)$$
Il vient alors que :
$$\ln \left(x^{2} \left(2x-6\right)\right)\ge \ln \left(12x-16\right)$$ équivaut successivement à
$$x^{2} \left(2x-6\right)\ge 12x-16$$
$$2x^{3} -6x^{2} -12x+16\ge 0$$.
Cette inéquation a été résolu à la question $$4$$.
Le domaine de définition impose que $$x\in \left]3;+\infty \right[$$ et l'inéquation est vraie si $$x\in \left[-2;1\right]\cup \left[4;+\infty \right[$$
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :