Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Résoudre une inéquation avec des logarithmes - Exercice 1
30 min
45
Pour chaque question, préciser l'ensemble de résolution de l'inéquation puis la résoudre.
Question 1
Correction
L'inéquation est définie si et seulement si
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Question 2
Correction
L'inéquation est définie si et seulement si :
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle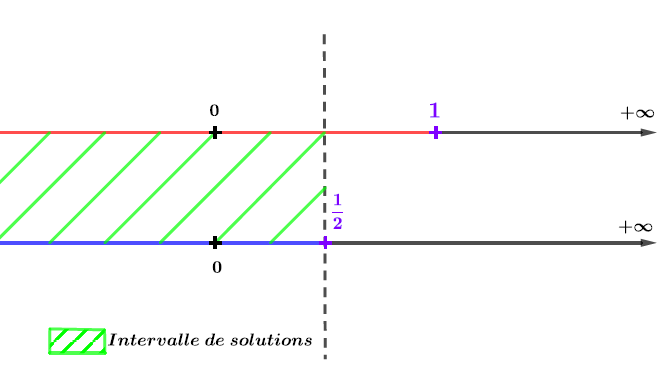
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle

Question 3
Correction
L'inéquation est définie si et seulement si
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Ainsi le domaine de définition est
Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Question 4
Correction
L'inéquation est définie si et seulement si
On fait l'intersection des deux intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant. ; et L'inéquation est vraie si
L'inéquation est vraie si
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
On fait l'intersection des deux intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant. ; et

Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 5
Correction
L'inéquation est définie si et seulement si
On fait l'intersection des trois intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant. ; et L'inéquation est vraie si .
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
On fait l'intersection des trois intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant. ; et

Le domaine de définition impose que et l'inéquation est vraie si . On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Question 6
Correction
L'inéquation est définie si et seulement si
On fait l'intersection des deux intervalles , ainsi le domaine de définition est
, on va tout mettre au même dénominateur.
Comme , le signe de dépend du dénominateur . On utilise le discriminant ; et
Autrement dit :
Le domaine de définition impose que et l'inéquation est vraie si .On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
On fait l'intersection des deux intervalles , ainsi le domaine de définition est
, on va tout mettre au même dénominateur.
Comme , le signe de dépend du dénominateur . On utilise le discriminant ; et

Autrement dit :
Le domaine de définition impose que et l'inéquation est vraie si .On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Question 7
Correction
L'inéquation est définie si et seulement si
On fait l'intersection des trois intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant.
; et L'inéquation est vraie si .
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
On fait l'intersection des trois intervalles, ainsi le domaine de définition est
Pour résoudre l'inéquation , on utilise le discriminant.
; et

Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.