Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Logarithme, primitives et suites - Exercice 2
40 min
65
Partie A.
Question 1
Soit la fonction définie sur par : . On note la courbe représentative de dans un repère orthonormé.
Démontrer que la courbe admet une asymptote horizontale.
Correction
La courbe admet la droite d’équation comme asymptote horizontale en .
Question 2
Déterminer la fonction dérivée de la fonction sur .
Correction
Soit que nous pouvons également écrire
est dérivable sur .
La fonction est définie si et seulement si .
De plus est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que
est dérivable sur .
La fonction est définie si et seulement si .
De plus est dérivable sur .
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que
Question 3
Étudier les variations de la fonction sur .
Correction
Nous savons que :
Pour tout , donc le signe de dépend de .
Il en résulte donc que :
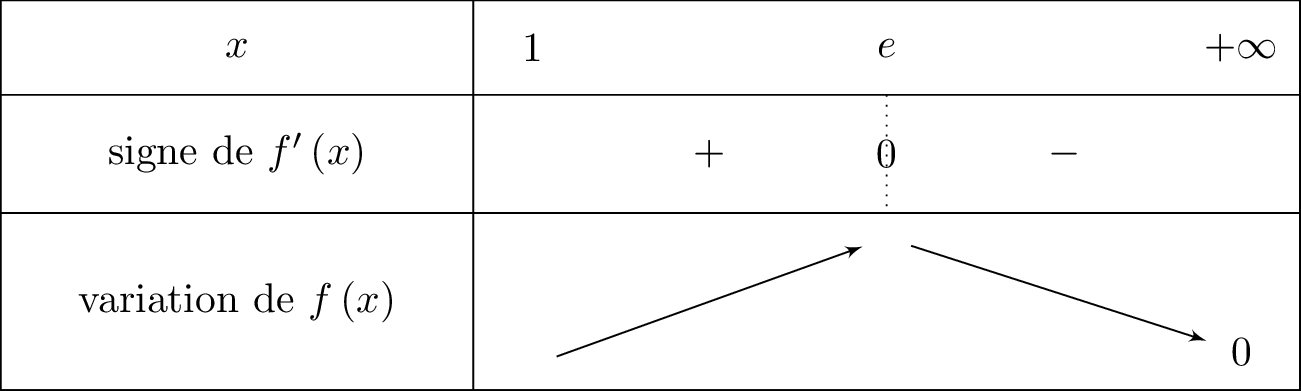
Pour tout , donc le signe de dépend de .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Question 4
Partie B.
On considère la suite définie par : pour tout entier naturel .
On considère la suite définie par : pour tout entier naturel .
Démontrer que . Interpréter graphiquement ce résultat.
Correction
Nous allons commencer par calculer une primitive de la fonction . Il vient alors que :
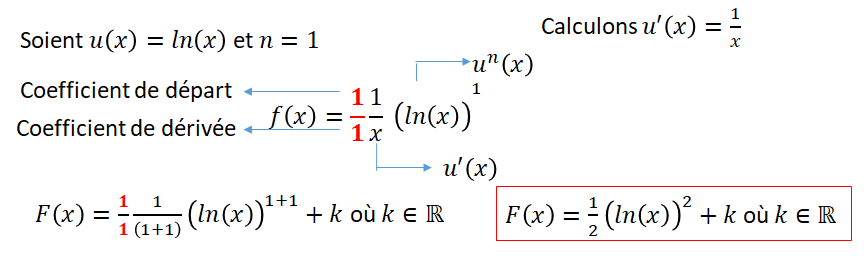 Ainsi :
Ainsi :

Question 5
Prouver que, pour tout entier naturel et pour tout nombre réel de l’intervalle , on a : .
Correction
Pour tout réel , on a :
équivaut successivement à :
car la fonction est croissante sur l'intervalle
car sur l'intervalle
Ainsi :
équivaut successivement à :
car la fonction est croissante sur l'intervalle
car sur l'intervalle
Ainsi :
Question 6
En déduire que, pour tout entier naturel , on a : .
Correction
Positivité de l'intégrale. Soient , et trois fonctions continues sur un intervalle
Si alors Si alors Si alors Si alors
Pour tout réel , d'après la question , on a : .D'après la positivité de l'intégrale, on a :
Il nous faut donc calculer :
Ainsi :
Pour tout entier naturel , la fonction a pour primitive la fonction .
Il en résulte donc que :
Nous allons factoriser maintenant l'expression par .
Finalement :
pour tout entier naturel , on a :
Question 7
Déterminer la limite de la suite .
Correction
et donc
Par produit :
Pour tout entier naturel , on a : et
D’après le théorème des gendarmes, que la suite est convergente et a pour limite .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.