Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
40 min
65
Question 1
On considère la fonction définie sur par : .
On note la courbe représentative de dans un repère orthonormé.
On note la courbe représentative de dans un repère orthonormé.
Déterminer la limite en de la fonction et interpréter graphiquement le résultat.
Correction
Nous pouvons écrire sous la forme :
Or : et de ce fait :
Il vient alors que :
On en déduit que la droite d’équation est asymptote verticale à la courbe .
Or : et de ce fait :
Il vient alors que :
On en déduit que la droite d’équation est asymptote verticale à la courbe .
Question 2
Démontrer que, pour tout appartenant à ,
Correction
- Soit :
Soit , on a :
Question 3
En déduire que l’axe des abscisses est une asymptote à la courbe représentative de la fonction au voisinage de .
Correction
D'après la question , nous pouvons écrire que :
On sait que :
On pose et ainsi par composition :
Il en résulte donc que :
Finalement :
On en déduit que l’axe des abscisses , c'est à dire , est une asymptote à la courbe représentative de la fonction au voisinage de .
On sait que :
On pose et ainsi par composition :
Il en résulte donc que :
Finalement :
On en déduit que l’axe des abscisses , c'est à dire , est une asymptote à la courbe représentative de la fonction au voisinage de .
Question 4
Calculer et
Correction
Ainsi
Question 5
On admet que est dérivable sur et on note sa fonction dérivée.
Démontrer que, pour tout appartenant à ,
Correction
est dérivable sur .
Ici on reconnaît la forme avec et . Pour dériver , on va utiliser la forme .
Ainsi et .
. On factorise maintenant par , cela nous donne :
Ici on reconnaît la forme avec et . Pour dériver , on va utiliser la forme .
Ainsi et .
. On factorise maintenant par , cela nous donne :
Question 6
Dresser alors le tableau de variation complet de .
Correction
Pour tout , on vérifie aisément que . Le signe de dépend alors .
Le tableau de variation complet de est alors donné ci-dessous :
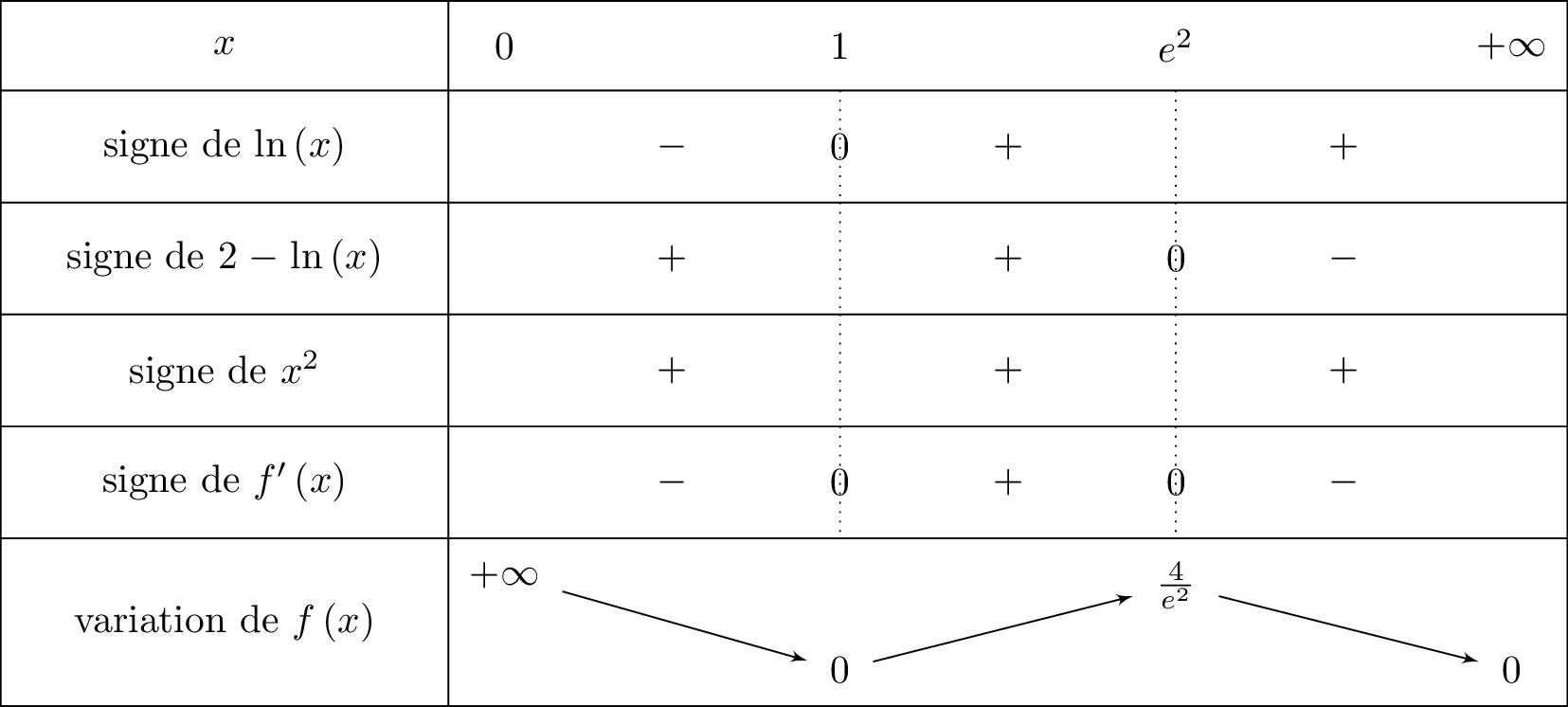
Le tableau de variation complet de est alors donné ci-dessous :

Question 7
Démontrer que l’équation admet une unique solution sur et donner un encadrement de d’amplitude .
Correction
Dans un premier temps, nous allons indiquer dans le tableau la valeur telle que .
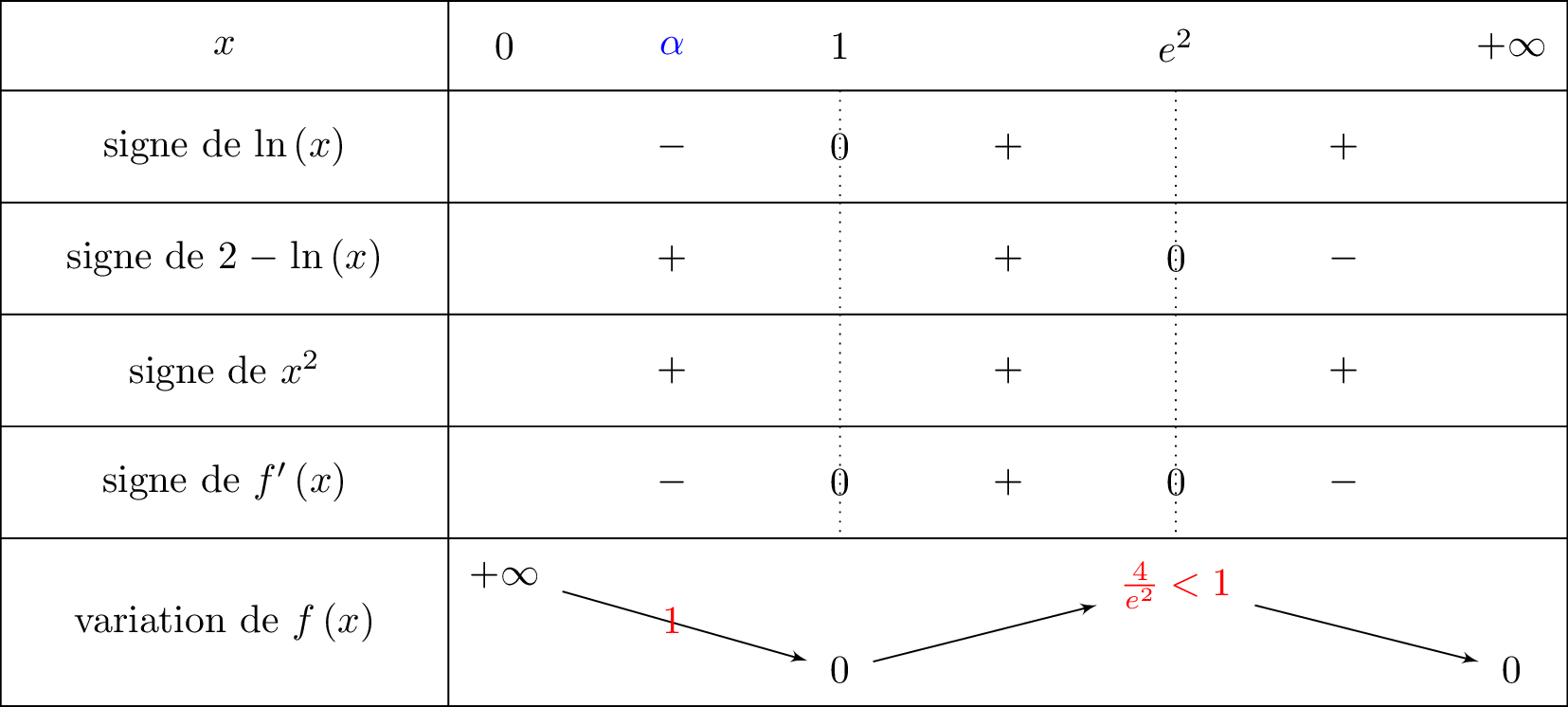
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :

- Sur , la fonction est continue et admet comme maximum.
La fonction est alors inférieur à sur l'intervalle
Donc l'équation n'a pas de solution sur cet intervalle. - Sur , la fonction est continue et strictement décroissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.