Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
45 min
70
La chocolaterie Delmas décide de commercialiser de nouvelles confiseries : des palets au chocolat en forme de goutte d’eau. Pour cela, elle doit fabriquer des moules sur mesure qui doivent répondre à la contrainte suivante : pour que cette gamme de bonbons soit rentable, la chocolaterie doit pouvoir en fabriquer au moins avec litre de pâte liquide au chocolat.
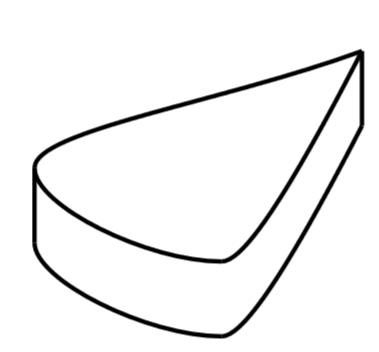 Partie A : modélisation par une fonction.
Partie A : modélisation par une fonction.
Le demi-contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction définie sur par : .
La représentation graphique de la fonction est donnée ci-dessous.
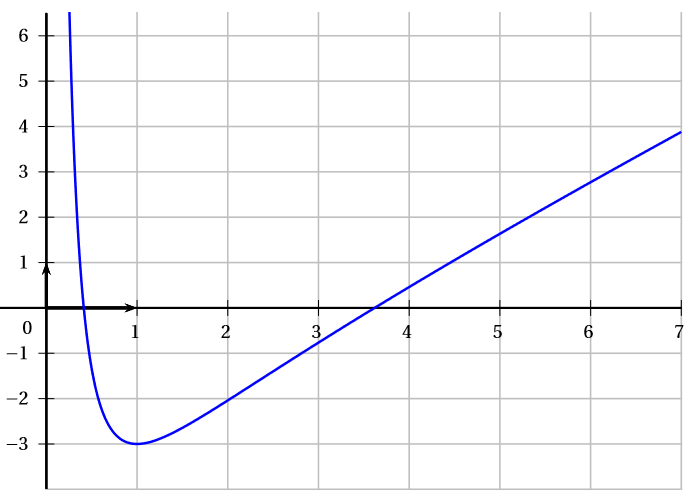 Le repère est orthogonal d’unité cm en abscisses et cm en ordonnées.
Le repère est orthogonal d’unité cm en abscisses et cm en ordonnées.

Le demi-contour de la face supérieure du palet sera modélisé par une portion de la courbe de la fonction définie sur par : .
La représentation graphique de la fonction est donnée ci-dessous.

Question 1
Soit la fonction définie sur par: . Calculer et la limite de en et .
Correction
De plus :
Question 2
Étudier les variations de sur . En déduire le signe de selon les valeurs de .
Correction
Soit
Ainsi :
Pour tout réel appartenant à l'intervalle , on vérifie aisément que :
On dresse ci-dessous le tableau variation complet de en intégrant les informations de la question .
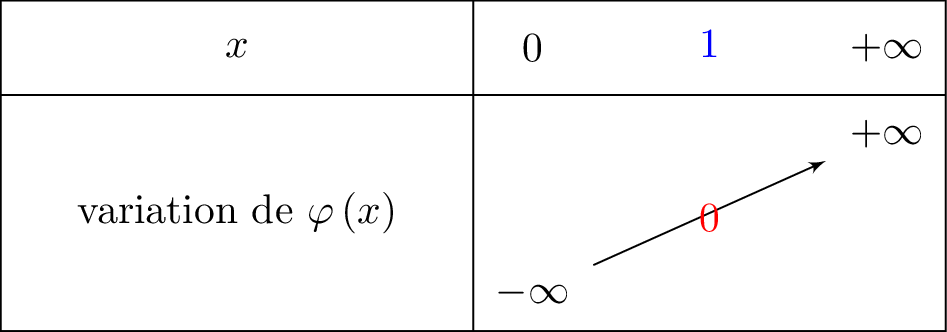 Il en résulte que :
Il en résulte que :
sur l'intervalle : sur l'intervalle : 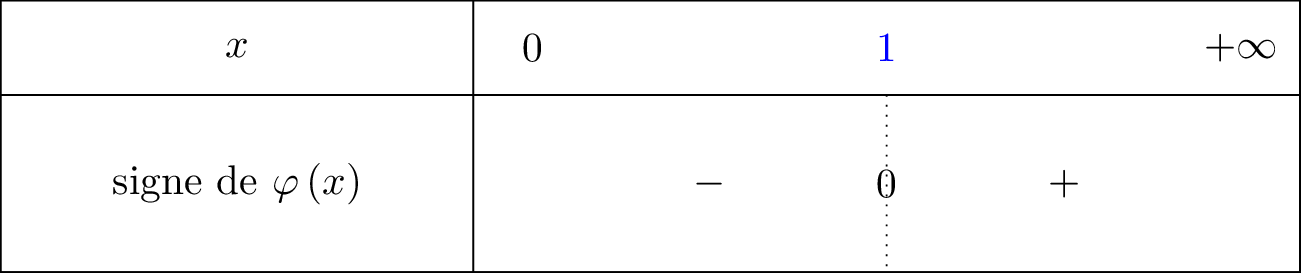
Ainsi :
Pour tout réel appartenant à l'intervalle , on vérifie aisément que :
On dresse ci-dessous le tableau variation complet de en intégrant les informations de la question .
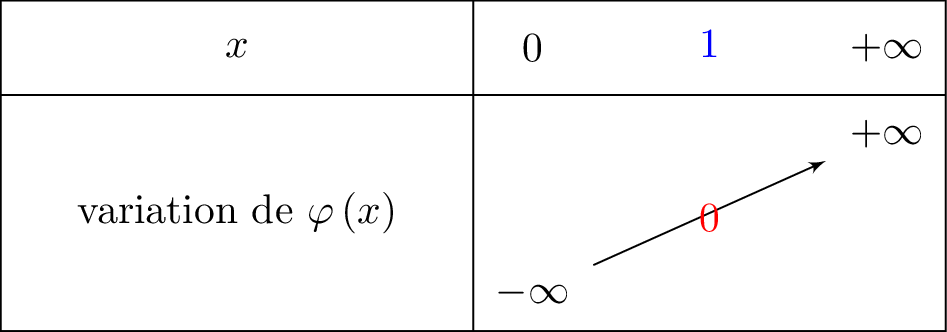

Question 3
Calculer les limites de aux bornes de son ensemble de définition.
Correction
Calcul de la limite en .
Calcul de la limite en .
Question 4
Montrer que sur : . En déduire le tableau de variation de .
Correction
Soit
est dérivable sur
Ici on reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
Ainsi :
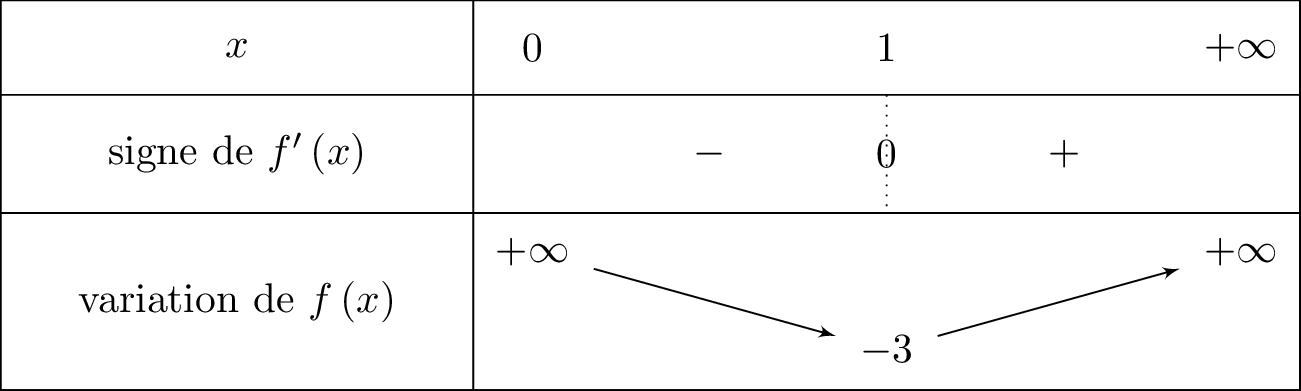
Pour tout réel appartenant à , on sait que . Il en résulte que le signe de est alors du signe de que l'on a déterminé à la question . En reprenant également les calculs de limites vues à la question , nous pouvons dresser le tableau de variation complet de .
est dérivable sur
Ici on reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
Ainsi :
Pour tout réel appartenant à , on sait que . Il en résulte que le signe de est alors du signe de que l'on a déterminé à la question . En reprenant également les calculs de limites vues à la question , nous pouvons dresser le tableau de variation complet de .

Question 5
Prouver que l’équation admet une unique solution sur . Déterminer à la calculatrice une valeur approchée de à près. On admettra que l’équation a également une unique solution sur avec à près.
Correction
Sur , la fonction est continue et strictement décroissante.
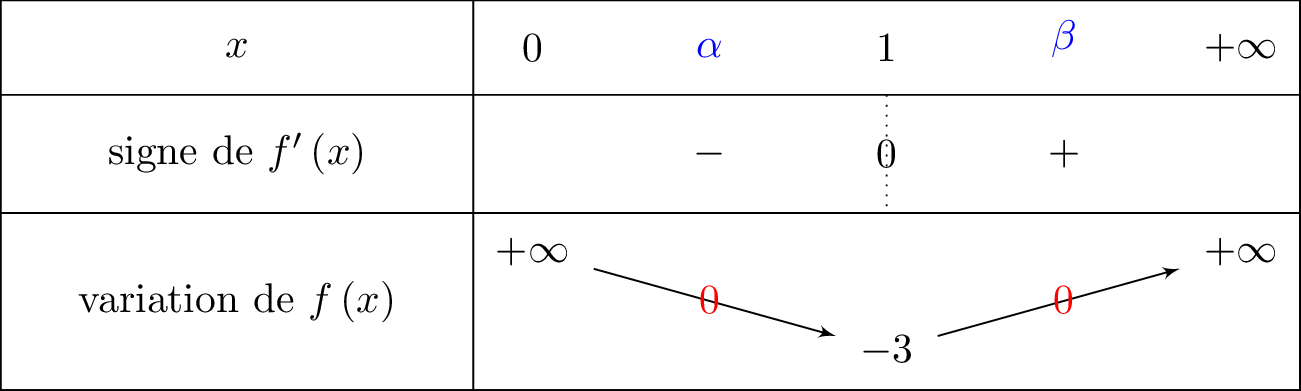 De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et . Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
On admettra que l’équation a également une unique solution sur avec à près.

A la calculatrice, on vérifie que :
et . Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
donc une valeur approchée est alors : .
On admettra que l’équation a également une unique solution sur avec à près.
Question 6
Soit la fonction définie sur par : .
Montrer que est une primitive de sur .
Montrer que est une primitive de sur .
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que :
Pour la dérivée de la fonction on va utiliser la forme .est dérivable sur , il vient alors :
. Nous mettons ensuite tout au même dénominateur.
Ainsi :
Question 7
Partie B: résolution du problème.
Dans cette partie, les calculs seront effectués avec les valeurs approchées à près de et de la partie A.
Dans cette partie, les calculs seront effectués avec les valeurs approchées à près de et de la partie A.
Pour obtenir la forme de la goutte, on considère la courbe représentative de la fonction restreinte à l’intervalle ainsi que son symétrique par rapport à l’axe des abscisses. Les deux courbes et délimitent la face supérieure du palet. Pour des raisons esthétiques, le chocolatier aimerait que ses palets aient une épaisseur de cm. Dans ces conditions, la contrainte de rentabilité serait-elle respectée?
Correction
Soit le domaine hachuré délimité par la courbe , l’axe des abscisses et les deux droites d’équations et .
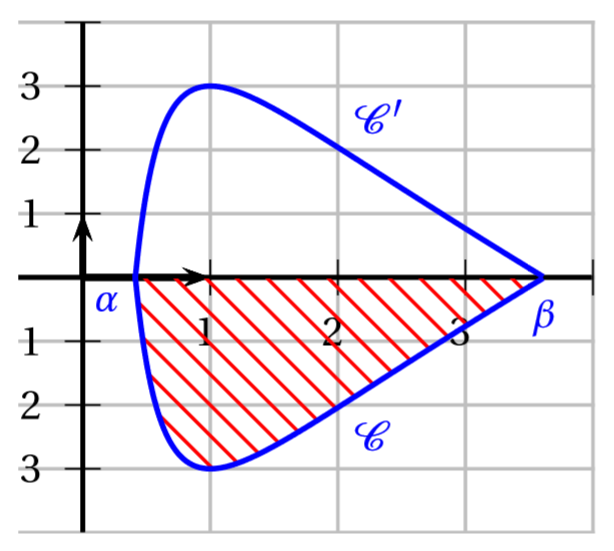 Sur l’intervalle , la fonction est négative, donc l’aire de est :
Sur l’intervalle , la fonction est négative, donc l’aire de est :
L’aire du domaine compris entre les deux courbes est U.A Une unité d’aire est égale à cm donc l’aire entre les deux courbes vaut environ cm. L’épaisseur du palet doit être de cm donc le volume du palet est d’environ cm. Le volume, en cm, de palets est donc , donc la chocolaterie peut fabriquer palets avec cm, soit litre de chocolat liquide.

unités d'aire
. (UA= Unités d'aires)L’aire du domaine compris entre les deux courbes est U.A Une unité d’aire est égale à cm donc l’aire entre les deux courbes vaut environ cm. L’épaisseur du palet doit être de cm donc le volume du palet est d’environ cm. Le volume, en cm, de palets est donc , donc la chocolaterie peut fabriquer palets avec cm, soit litre de chocolat liquide.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.