Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 5
25 min
40
On considère la fonction définie sur , .
Question 1
Déterminer les limites de en et en .
Correction
.
. On pose , ainsi .
Par composition .
Ainsi
On en déduit que la courbe admet une asymptote verticale d'équation .
.
. On pose , ainsi .
Par composition .
Ainsi
. On pose , ainsi .
Par composition .
Ainsi
On en déduit que la courbe admet une asymptote verticale d'équation .
.
. On pose , ainsi .
Par composition .
Ainsi
Question 2
Etudiez les variations de sur .
Correction
On reconnait la forme . On et
. Nous avons tout mis au même dénominateur c'est à dire sur .
. On rappelle que :
Ainsi :
Or donc et .
Donc le signe de dépend du numérateur .
On considère le trinôme . et donc car
On peut donner alors le tableau de variation de en indiquant les limites.
Il vient alors que :
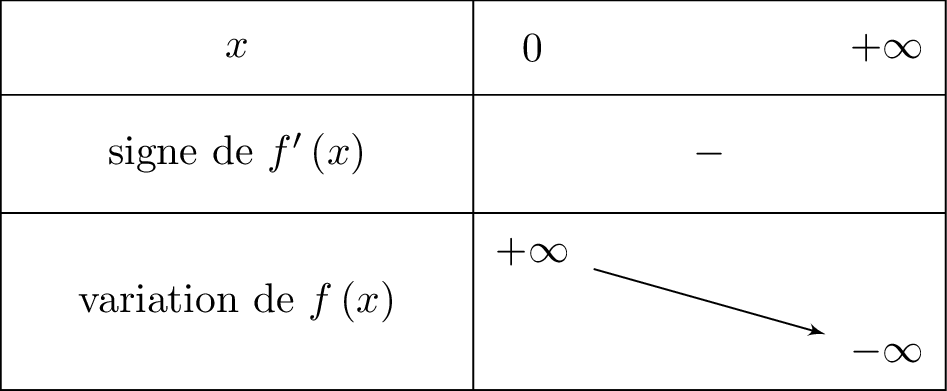
Question 3
Montrer qu'il existe un unique réel tel que .
Correction
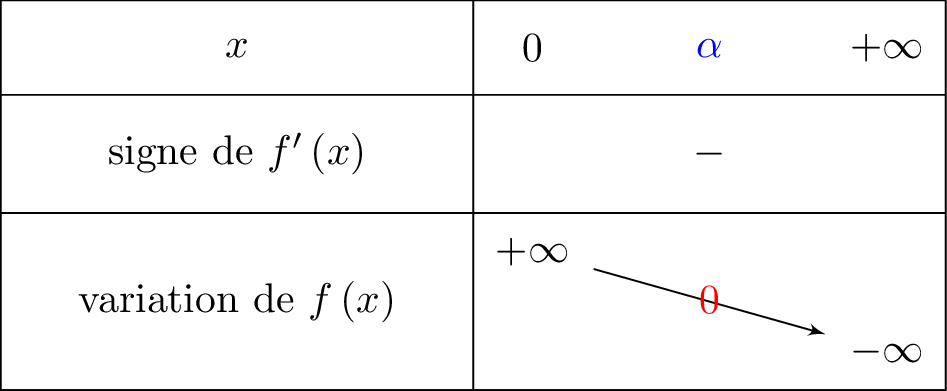
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Question 4
Déterminer une valeur approchée de à près.
Correction
A la calculatrice, on vérifie que
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 5
En déduire le signe de .
Correction
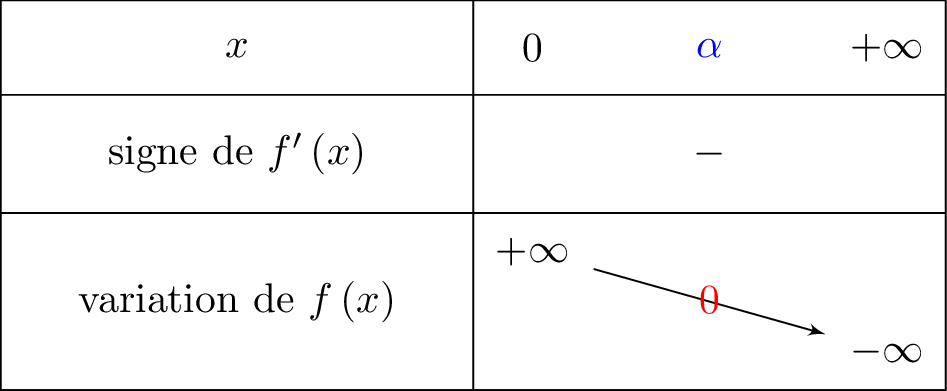
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.