Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 2
30 min
45
On considère la fonction définie sur l'intervalle par .
Question 1
Etudier les variations de la fonction sur l'intervalle .
Correction
Soit : .
Calculons sur la dérivée de .
Ici pas besoin de mettre tout au même dénominateur car les deux expressions sont strictement positives.
En effet, comme alors et .
Ainsi sur , et donc la fonction est strictement croissante sur .
Calculons sur la dérivée de .
Ici pas besoin de mettre tout au même dénominateur car les deux expressions sont strictement positives.
En effet, comme alors et .
Ainsi sur , et donc la fonction est strictement croissante sur .
Question 2
Justifier qu'il existe un unique réel tel que .
Donner une valeur approchée de à près.
Donner une valeur approchée de à près.
Correction
Commençons par calculer les limites aux bornes du domaine de définition.
On en déduit que la courbe admet une asymptote verticale d'équation .
Dressons le tableau de variation en intégrant les limites :
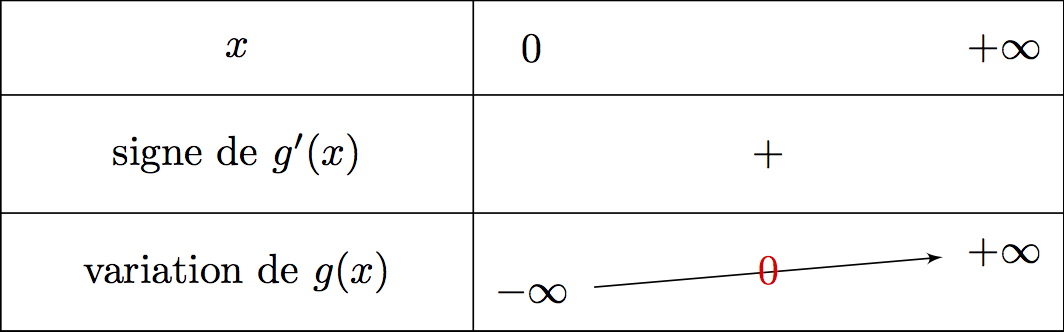 Sur , la fonction est continue et strictement croissante.
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
On en déduit que la courbe admet une asymptote verticale d'équation .
Dressons le tableau de variation en intégrant les limites :

De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 3
En déduire le signe de la fonction sur l'intervalle .
Correction
Sur , la fonction est continue et strictement croissante et .
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Donc pour tout et pour tout .
On résume cela dans un tableau de signe :

Question 4
On considère la fonction définie sur l'intervalle par .
Déterminer les limites de la fonction en et en .
Correction
et
On en déduit que la courbe admet une asymptote verticale d'équation .
Question 5
Justifier que a le même signe que .
Correction
Soit : .
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à
On factorise maintenant le numérateur par , ainsi :
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
On factorise maintenant le numérateur par , ainsi :
Question 6
En déduire le tableau de variation de la fonction .
Correction
Comme et que alors est du même signe que .
On en déduit facilement le tableau de variation de la fonction :
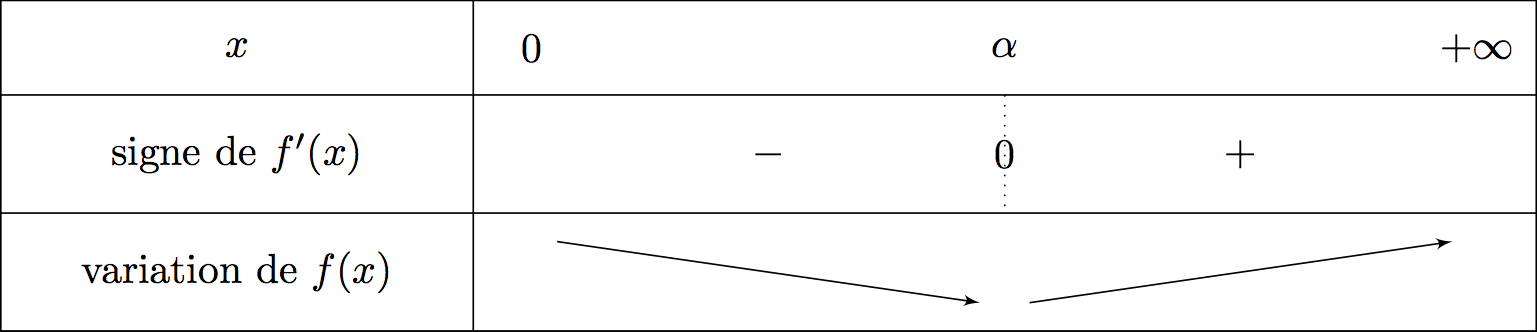
On en déduit facilement le tableau de variation de la fonction :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.