Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Etudes de fonctions - Exercice 1
30 min
45
Partie A
Soit la fonction définie sur par .
Soit la fonction définie sur par .
Question 1
Calculer les limites de en et .
Correction
.
Il en résulte que la courbe admet une asymptote verticale d'équation .
Question 2
Etudiez les variations de .
Correction
est dérivable sur . On obtient alors :
.
Ici, pas besoin de mettre tout au même dénominateur. En effet, on sait que , de ce fait et .
Il en résulte que pour tout réel appartenant à , on a .
Nous traduisons cela dans le tableau de variation ci-dessous :
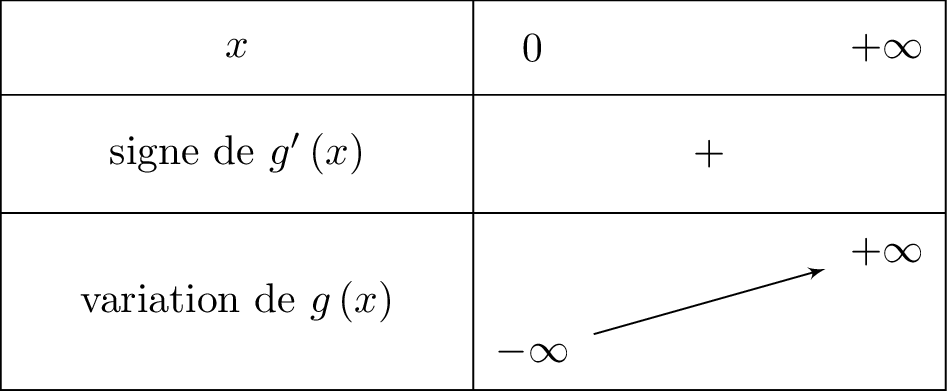
.
Ici, pas besoin de mettre tout au même dénominateur. En effet, on sait que , de ce fait et .
Il en résulte que pour tout réel appartenant à , on a .
Nous traduisons cela dans le tableau de variation ci-dessous :

Question 3
Vérifier que
Correction
On a :
ainsi
ainsi
Question 4
En déduire le signe de sur .
Correction
On sait que . Nous intégrons cette information dans le tableau de variation, ce qui nous donne :
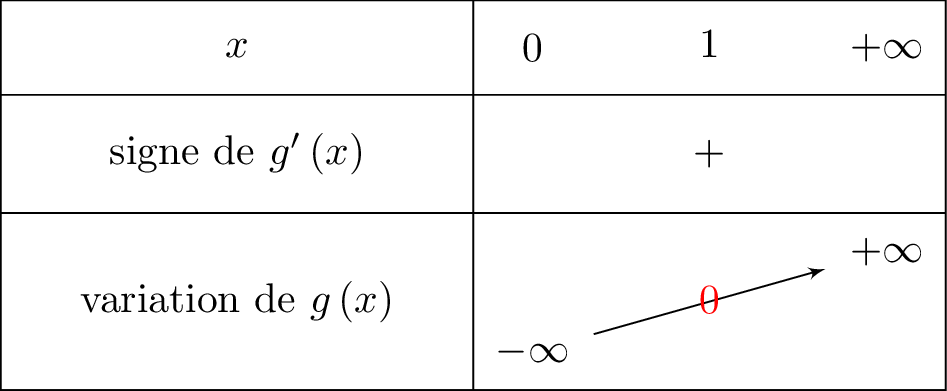 Sur , la fonction est continue et strictement croissante.
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que . Ici .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
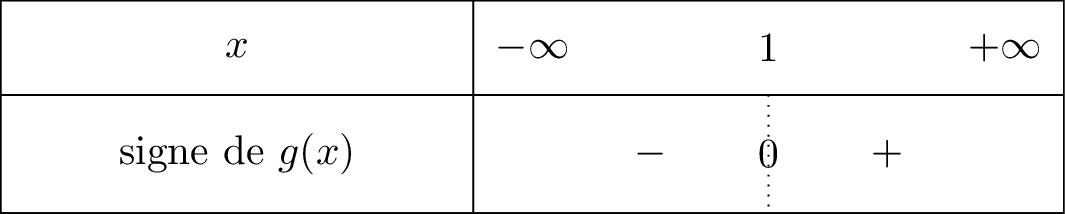
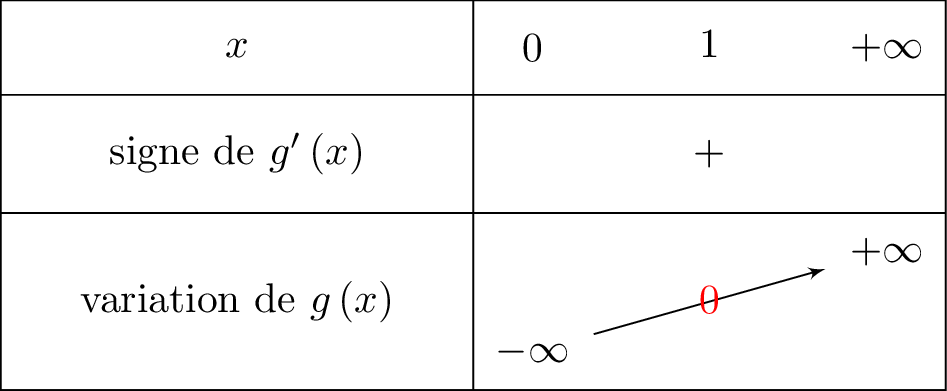
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que . Ici .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 5
Partie B
On considère la fonction définie sur par :
On considère la fonction définie sur par :
Calculer la limite de en . Que peut-on en déduire graphiquement?
Correction
.
De plus, .
Finalement :
Il en résulte que la courbe admet une asymptote verticale d'équation .
De plus, .
Finalement :
Il en résulte que la courbe admet une asymptote verticale d'équation .
Question 6
Calculer la limite de en .
Correction
.
Finalement :
Question 7
Montrer que pour tout appartenant à
Correction
Soit :
est dérivable sur .
On reconnaît la forme avec et et .
Ainsi et et .
Il vient alors que :
. Nous allons tout mettre au même dénominateur, ce qui donne :
Ainsi :
Finalement :
est dérivable sur .
On reconnaît la forme avec et et .
Ainsi et et .
Il vient alors que :
. Nous allons tout mettre au même dénominateur, ce qui donne :
Ainsi :
Finalement :
Question 8
En déduire les variations de sur .
Correction
On sait que :
Comme appartient à alors . Il en résulte que le signe de ne dépend que de son numérateur donc ici la fonction . Cela signifie que le signe de est le même que celui de la fonction .
Or d'après la question , on connaît le signe de . Nous pouvons donc facilement dresser le tableau de variation de .
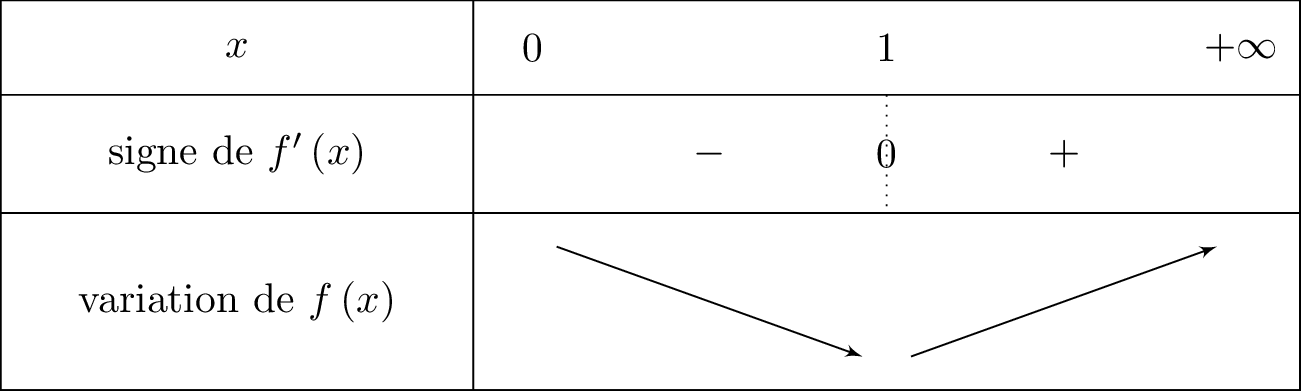
Comme appartient à alors . Il en résulte que le signe de ne dépend que de son numérateur donc ici la fonction . Cela signifie que le signe de est le même que celui de la fonction .
Or d'après la question , on connaît le signe de . Nous pouvons donc facilement dresser le tableau de variation de .

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.