Fonction logarithme népérien

Epreuve d'enseignement de spécialité Session 8 Juin 2021 Exercice A - Exercice 1

45 min
70
Partie A :\red{\text{Partie A :}}
On désigne par hh la fonction définie sur l’intervalle ]0;+∞[\left]0;+\infty\right[ par : h(x)=1+ln⁡(x)x2h\left(x\right)=1+\frac{\ln \left(x\right)}{x^{2} }
On admet que la fonction hh est dérivable sur ]0;+∞[\left]0;+\infty\right[ et on note h′h' sa fonction dérivée.
Question 1

Déterminer les limites de hh en 00 et en +∞+\infty .

Correction
D’une part :\blue{\text{D'une part :}}
lim⁡x→0+ln⁡(x)=−∞\lim\limits_{x\to 0^{+} } \ln \left(x\right)=-\infty
lim⁡x→0+1+ln⁡(x)x2=lim⁡x→0+1+1x2×ln⁡(x){\mathop{\lim }\limits_{x\to 0^{+} }} 1+\frac{\ln \left(x\right)}{x^{2} } ={\mathop{\lim }\limits_{x\to 0^{+} }} 1+\frac{1}{x^{2} } \times \ln \left(x\right)
lim⁡x→0+1x2=+∞{\mathop{\lim }\limits_{x\to 0^{+} }} \frac{1}{x^{2} } =+\infty et lim⁡x→0+ln⁡(x)=−∞\lim\limits_{x\to 0^{+} } \ln \left(x\right)=-\infty
Il en résulte donc que, par produit, lim⁡x→0+1x2×ln⁡(x)=−∞{\mathop{\lim }\limits_{x\to 0^{+} }} \frac{1}{x^{2} } \times \ln \left(x\right)=-\infty
Ainsi : lim⁡x→0+1+1x2×ln⁡(x)=−∞{\mathop{\lim }\limits_{x\to 0^{+} }} 1+\frac{1}{x^{2} } \times \ln \left(x\right)=-\infty
Finalement :
lim⁡x→0+h(x)=−∞{\mathop{\lim }\limits_{x\to 0^{+} }} h\left(x\right)=-\infty

D’autre part :\blue{\text{D'autre part :}}
    Pour tout nombre entier nn strictement positif, on a :
  • lim⁡x→+∞ln⁡(x)xn=0\lim\limits_{x\to +\infty } \frac{\ln \left(x\right)}{x^{n} }=0
    • lim⁡x→+∞1=1lim⁡x→+∞ln⁡(x)x2=0}par addition\left. \begin{array}{ccc} {\lim\limits_{x\to +\infty }1} & {=} & {1 } \\ {\lim\limits_{x\to +\infty } \frac{\ln \left(x\right)}{x^{2} }} & {=} & {0 } \end{array}\right\}{\red{\text{par addition}}}
    lim⁡x→+∞1+ln⁡(x)x2=1{\mathop{\lim }\limits_{x\to +\infty }} 1+\frac{\ln \left(x\right)}{x^{2} }=1

    Finalement : \purple{\text{Finalement : }}
    lim⁡x→+∞h(x)=1{\mathop{\lim }\limits_{x\to +\infty }} h\left(x\right)=1
    Question 2

    Montrer que, pour tout nombre réel xx de ]0;+∞[\left]0;+\infty\right[, h′(x)=1−2ln⁡(x)x3h'\left(x\right)=\frac{1-2\ln \left(x\right)}{x^{3} }

    Correction
    hh est dérivable sur ]0;+∞[\left]0;+\infty\right[
    Ici on reconnaît la forme (w+uv)′=w′+u′v−uv′v2\color{red}\boxed{\left(w+\frac{u}{v} \right)^{'} =w'+\frac{u'v-uv'}{v^{2} }} avec w(x)=1w\left(x\right)=1 ; u(x)=ln⁡(x)u\left(x\right)=\ln \left(x\right) et v(x)=x2v\left(x\right)=x^{2}.
    Ainsi w′(x)=0w'\left(x\right)=0 ; u′(x)=1xu'\left(x\right)=\frac{1}{x} et v′(x)=2xv'\left(x\right)=2x.
    Il vient alors que :
    h′(x)=1x×x2−ln⁡(x)×2x(x2)2h'\left(x\right)=\frac{\frac{1}{x} \times x^{2} -\ln \left(x\right)\times 2x}{\left(x^{2} \right)^{2} }
    h′(x)=x2x−2xln⁡(x)x4h'\left(x\right)=\frac{\frac{x^{2} }{x} -2x\ln \left(x\right)}{x^{4} }
    h′(x)=x−2xln⁡(x)x4h'\left(x\right)=\frac{x-2x\ln \left(x\right)}{x^{4} }     \;\; On factorise par xx le numérateur et le dénominateur.
    h′(x)=x×(1−2ln⁡(x))x×x3h'\left(x\right)=\frac{x\times \left(1-2\ln \left(x\right)\right)}{x\times x^{3} }     \;\; On simplifie par xx le numérateur et le dénominateur.
    Finalement : \purple{\text{Finalement : }}
    h′(x)=1−2ln⁡(x)x3h'\left(x\right)=\frac{1-2\ln \left(x\right)}{x^{3} }

    Question 3

    En déduire les variations de la fonction hh sur l’intervalle ]0;+∞[\left]0;+\infty\right[ .

    Correction
    Soit x∈]0;+∞[x\in \left]0;+\infty\right[
    D'après la question 22 nous savons que : h′(x)=1−2ln⁡(x)x3h'\left(x\right)=\frac{1-2\ln \left(x\right)}{x^{3} }
    Pour tout réel x∈]0;+∞[x\in \left]0;+\infty\right[, on peut affirmer aisément que x3>0x^{3}>0.
    Le signe de ff' dépend alors du signe du numérateur 1−2ln⁡(x)1-2\ln \left(x\right) .
    1−2ln⁡(x)≥01-2\ln \left(x\right)\ge 0 équivaut successivement à :
    −2ln⁡(x)≥−1-2\ln \left(x\right)\ge -1
    ln⁡(x)≤−1−2\ln \left(x\right)\le \frac{-1}{-2}
    ln⁡(x)≤12\ln \left(x\right)\le \frac{1}{2}
    x≤e12x\le e^{\frac{1}{2} }
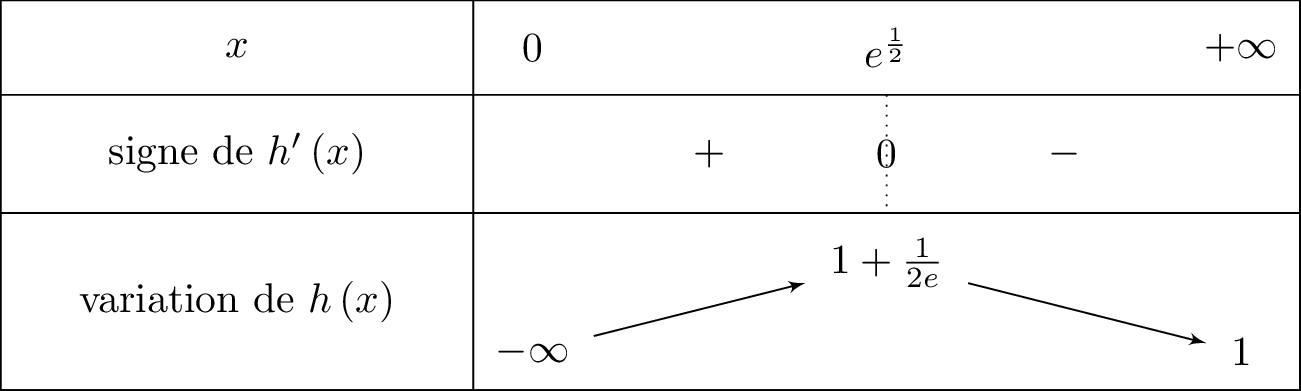
    Il en résulte donc que :
    • si x∈]0;e12]x\in\left]0;e^{\frac{1}{2} } \right] alors h′(x)≥0h'\left(x\right)\ge0 et donc hh est croissante sur cet intervalle.
    • si x∈[e12;+∞[x\in\left[e^{\frac{1}{2} } ;+\infty\right[ alors h′(x)≤0h'\left(x\right)\le0 et donc hh est décroissante sur cet intervalle.
    Nous traduisons toutes ces informations dans le tableau de variation ci-dessous :
    De plus :
    h(e12)=1+ln⁡(e12)(e12)2h\left(e^{\frac{1}{2} } \right)=1+\frac{\ln \left(e^{\frac{1}{2} } \right)}{\left(e^{\frac{1}{2} } \right)^{2} }
    h(e12)=1+ln⁡(e12)e12×2h\left(e^{\frac{1}{2} } \right)=1+\frac{\ln \left(e^{\frac{1}{2} } \right)}{e^{\frac{1}{2} \times 2} }
    h(e12)=1+ln⁡(e12)e1h\left(e^{\frac{1}{2} } \right)=1+\frac{\ln \left(e^{\frac{1}{2} } \right)}{e^{1} }
    h(e12)=1+12eh\left(e^{\frac{1}{2} } \right)=1+\frac{\frac{1}{2} }{e}
    h(e12)=1+12×1eh\left(e^{\frac{1}{2} } \right)=1+\frac{1}{2} \times \frac{1}{e}
    h(e12)=1+12eh\left(e^{\frac{1}{2} } \right)=1+\frac{1}{2e}
    h(e12)≈1,18h\left(e^{\frac{1}{2} } \right)\approx 1,18
    Question 4

    Montrer que l’équation h(x)=0h\left(x\right) = 0 admet une solution unique α appartenant à ]0;+∞[\left]0;+\infty\right[ et vérifier que : 12<α<1\frac{1}{2}< \alpha < 1

    Correction
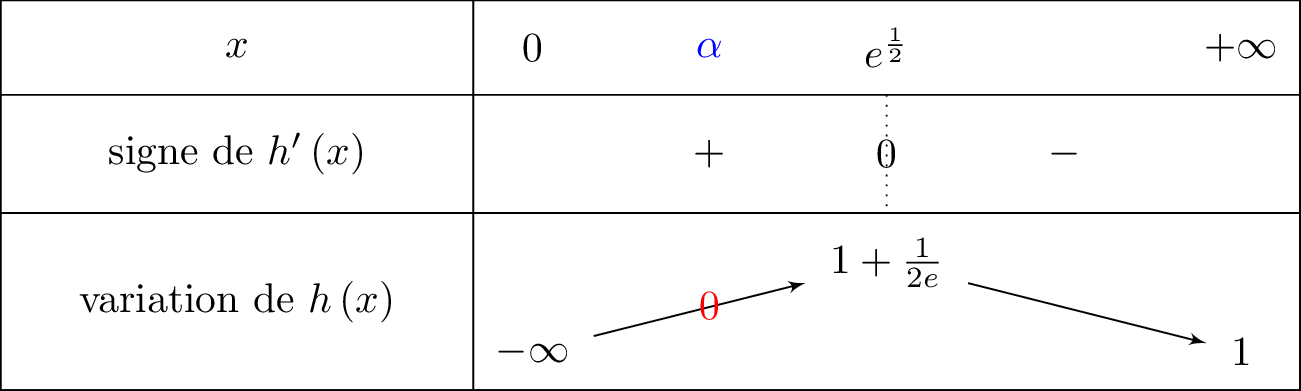
    • Sur [e12;+∞[\left[e^{\frac{1}{2} };+\infty\right[ , la fonction hh est continue et admet 11 comme minimum.
      La fonction hh est strictement positive.
      Donc l'équation h(x)=0h\left(x\right)=0 n'a pas de solution sur cet intervalle.
    • Sur ]0;e12]\left]0;e^{\frac{1}{2} }\right] , la fonction hh est continue et strictement croissante.
      De plus, lim⁡x→0+h(x)=−∞{\mathop{\lim }\limits_{x\to 0^{+} }} h\left(x\right)=-\infty et h(e12)=1+12eh\left(e^{\frac{1}{2} } \right)=1+\frac{1}{2e}
      Or 0∈]−∞;1+12e]0 \in \left]-\infty;1+\frac{1}{2e}\right] , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution α\alpha dans ]0;e12]\left]0;e^{\frac{1}{2} }\right] tel que h(x)=0h\left(x\right) = 0.
    Plus précisément, nous avons h(12)≈−1,8<0h\left(\frac{1}{2} \right)\approx -1,8<0 et h(1)=1>0h\left(1 \right)=1>0
    Finalement, l'équation h(x)=0h\left(x\right)=0 admet une unique solution α\alpha tel que : 12<α<1\frac{1}{2}< \alpha < 1
    Question 5

    Déterminer le signe de h(x)h\left(x\right) pour xx appartenant à ]0;+∞[\left]0;+\infty\right[ .

    Correction
    Sur [e12;+∞[\left[e^{\frac{1}{2} };+\infty\right[ , la fonction hh est continue et admet 11 comme minimum. La fonction hh est strictement positive.
    Sur ]0;e12]\left]0;e^{\frac{1}{2} }\right], la fonction hh est continue et strictement croissante et h(α)=0h(\alpha) = 0
    Donc h(x)≤0h(x)\le0 pour tout x∈]0;α]x\in\left]0;\alpha\right] et h(x)≥0h(x)\ge0 pour tout x∈[α;e12]x\in\left[\alpha;e^{\frac{1}{2} }\right]
    On résume cela dans un tableau de signe :
    Question 6
    Partie B :\red{\text{Partie B :}}
    On désigne par f1f_{1} et f2f_{2} les fonctions définies sur ]0;+∞[\left]0;+\infty\right[ par : f1(x)=x−1−ln⁡(x)x2f_{1} \left(x\right)=x-1-\frac{\ln \left(x\right)}{x^{2} } et f2(x)=x−2−2ln⁡(x)x2f_{2} \left(x\right)=x-2-\frac{2\ln \left(x\right)}{x^{2} }
    On note C1\mathscr{C_1} et C2\mathscr{C_2} les représentations graphiques respectives de f1f_{1} et f2f_{2} dans un repère (O;i→;j→)\left(O;\overrightarrow{i} ;\overrightarrow{j} \right) .

    Montrer que, pour tout nombre réel xx appartenant à ]0;+∞[\left]0;+\infty\right[, on a : f1(x)−f2(x)=h(x)f_{1} \left(x\right)-f_{2} \left(x\right)=h\left(x\right)

    Correction
    Soit x∈]0;+∞[x\in \left]0;+\infty\right[
    f1(x)−f2(x)=x−1−ln⁡(x)x2−(x−2−2ln⁡(x)x2)f_{1} \left(x\right)-f_{2} \left(x\right)=x-1-\frac{\ln \left(x\right)}{x^{2} } -\left(x-2-\frac{2\ln \left(x\right)}{x^{2} } \right)
    f1(x)−f2(x)=x−1−ln⁡(x)x2−x+2+2ln⁡(x)x2f_{1} \left(x\right)-f_{2} \left(x\right)=x-1-\frac{\ln \left(x\right)}{x^{2} } -x+2+\frac{2\ln \left(x\right)}{x^{2} }
    f1(x)−f2(x)=1+ln⁡(x)x2f_{1} \left(x\right)-f_{2} \left(x\right)=1+\frac{\ln \left(x\right)}{x^{2} }
    Ainsi :
    f1(x)−f2(x)=h(x)f_{1} \left(x\right)-f_{2} \left(x\right)=h \left(x\right)

    Question 7

    Déduire des résultats de la Partie 11 la position relative des courbes C1\mathscr{C_1} et C2\mathscr{C_2} .
    On justifiera que leur unique point d’intersection a pour coordonnées (α;α)\left(\alpha ; \alpha \right).
    On rappelle que α\alpha est l’unique solution de l’équation h(x)=0h\left(x\right) = 0.

    Correction
    Soit x∈]0;+∞[x\in \left]0;+\infty\right[
    D'après la question 66, nous avons vu que : f1(x)−f2(x)=h(x)f_{1} \left(x\right)-f_{2} \left(x\right)=h \left(x\right)
    De plus, d'après la question nous connaissons le signe de h(x)h \left(x\right).
  • Sur ]0;α[\left]0;\alpha\right[ on sait que h(x)<0h \left(x\right)<0 et de ce fait f1(x)−f2(x)<0f_{1} \left(x\right)-f_{2} \left(x\right)<0 ainsi f1(x)<f2(x)f_{1} \left(x\right)<f_{2} \left(x\right) .
    On peut alors conclure que sur ]0;α[\left]0;\alpha\right[ la courbe C1\mathscr{C_1} est en dessous de la courbe C2\mathscr{C_2}
  • Sur ]α;+∞[\left]\alpha;+\infty\right[ on sait que h(x)>0h \left(x\right)>0 et de ce fait f1(x)−f2(x)>0f_{1} \left(x\right)-f_{2} \left(x\right)>0 ainsi f1(x)>f2(x)f_{1} \left(x\right)>f_{2} \left(x\right) .
    On peut alors conclure que sur ]0;α[\left]0;\alpha\right[ la courbe C1\mathscr{C_1} est au-dessus de la courbe C2\mathscr{C_2}
  • Si x=αx=\alpha alors h(α)=0h \left(\alpha\right)=0 ce qui permet de dire que f1(α)=f2(α)f_{1} \left(\alpha\right)=f_{2} \left(\alpha\right) . Les courbes C1\mathscr{C_1} et C2\mathscr{C_2} sont sécantes au point d'abscisse α\alpha .
    • Il nous faut donc calculer l'ordonnée et donc pour cela il faut calculer, par exemple, f1(α)f_{1} \left(\alpha\right) .
    Il vient alors que :
    f1(α)=α−1−ln⁡(α)α2f_{1} \left(\alpha \right)=\alpha -1-\frac{\ln \left(\alpha \right)}{\alpha ^{2} }
    f1(α)=α−(1+ln⁡(α)α2)f_{1} \left(\alpha \right)=\alpha -\left(1+\frac{\ln \left(\alpha \right)}{\alpha ^{2} } \right)
    f1(α)=α−h(α)f_{1} \left(\alpha \right)=\alpha -h\left(\alpha \right)
    D'après la question 44, nous avons montré que h(α)=0h\left(\alpha \right)=0 ce qui permet de conclure que α−h(α)=α\alpha -h\left(\alpha \right)=\alpha
    Il en résulte donc que :
    f1(α)=αf_{1} \left(\alpha \right)=\alpha

    On rappelle donc que :
  • Si x=αx=\alpha alors h(α)=0h \left(\alpha\right)=0 ce qui permet de dire que f1(α)=f2(α)f_{1} \left(\alpha\right)=f_{2} \left(\alpha\right) . Les courbes C1\mathscr{C_1} et C2\mathscr{C_2} sont sécantes au point d'abscisse α\alpha .
    Le point d'intersection a pour coordonnées (α;f1(α))\left(\alpha ;f_{1} \left(\alpha \right) \right) ou encore (α;α)\left(\alpha ; \alpha \right)