Fonction logarithme népérien
Epreuve d'enseignement de spécialité Session 7 Juin 2021 Exercice A - Exercice 1
45 min
70
désigne une fonction définie et dérivable sur .
On donne ci-dessous la courbe représentative de la fonction dérivée .
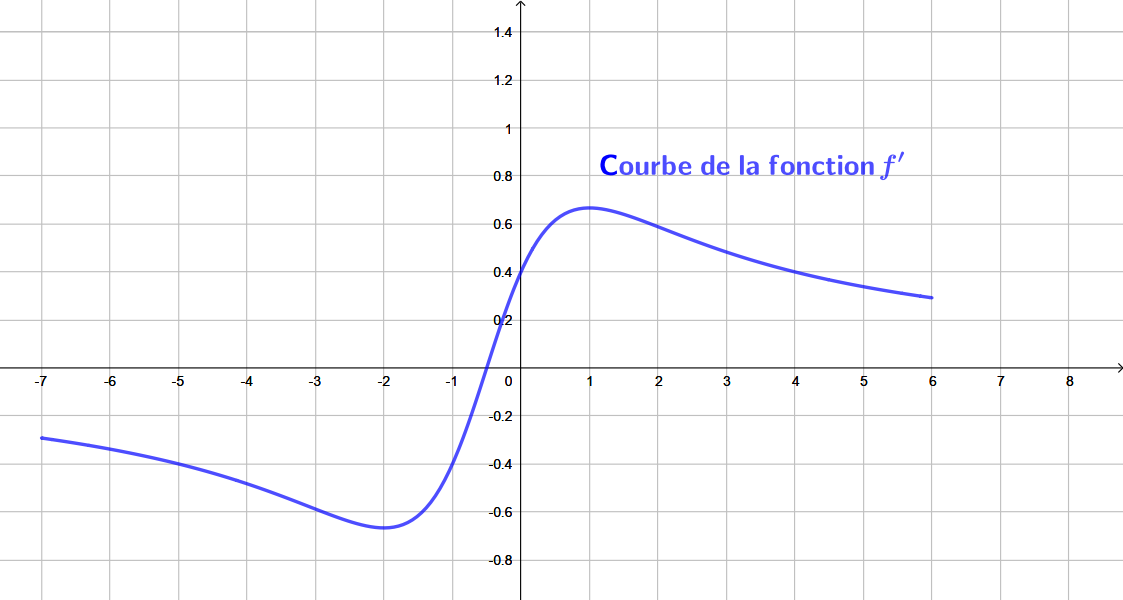
On donne ci-dessous la courbe représentative de la fonction dérivée .

Question 1
Déterminer le coefficient directeur de la tangente à la courbe de la fonction en .
Correction
Le nombre dérivée de la fonction au point est par définition le coefficient directeur de la tangente à la courbe représentative de au point d’abscisse .
Il se note .
D'après la lecture graphique, on lit alors que :
Il se note .
D'après la lecture graphique, on lit alors que :

Question 2
Donner les variations de la fonction dérivée .
Correction

- si alors est décroissante sur cet intervalle.
- si alors est croissante sur cet intervalle.
- si alors est décroissante sur cet intervalle.

Question 3
En déduire un intervalle sur lequel est convexe.
Correction
Pour étudier la convexité de la fonction , nous allons utiliser les variations de .
D'après le tableau de variation de , on en déduit :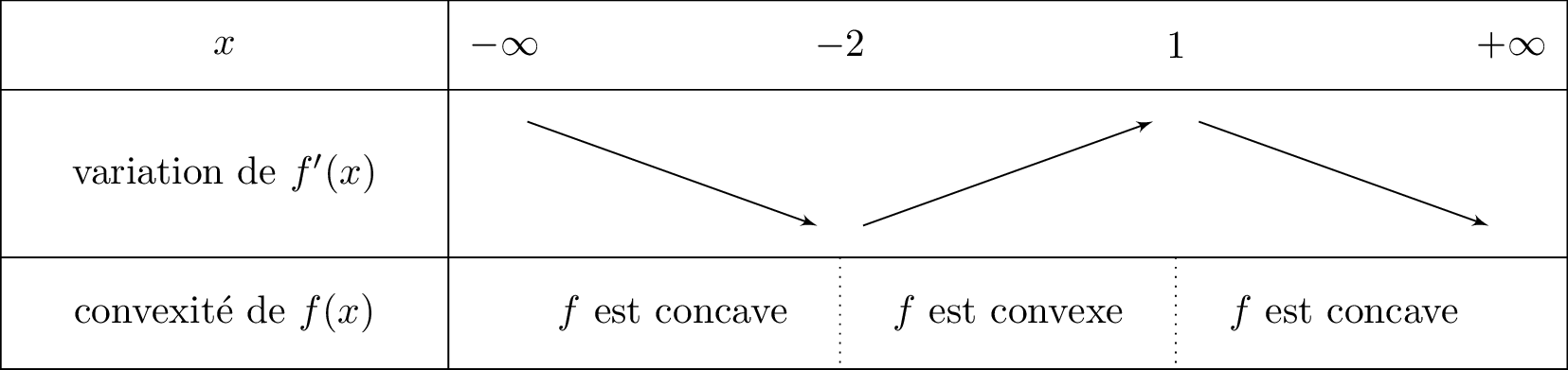 La fonction est convexe sur l'intervalle .
La fonction est convexe sur l'intervalle .
- Si est croissante alors est convexe sur
- Si est décroissante alors est concave sur

Question 4
La fonction est définie sur par .
Calculer la limite de la fonction en .
Correction
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Question 5
Calculer la limite de la fonction en .
Correction
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Question 6
Déterminer une expression de la fonction dérivée de pour tout .
Correction
La fonction est définie sur par .
La fonction est dérivable sur .
Ainsi :
La fonction est dérivable sur .
Ainsi :
Question 7
En déduire le tableau des variations de . On veillera à placer les limites dans ce tableau.
Correction
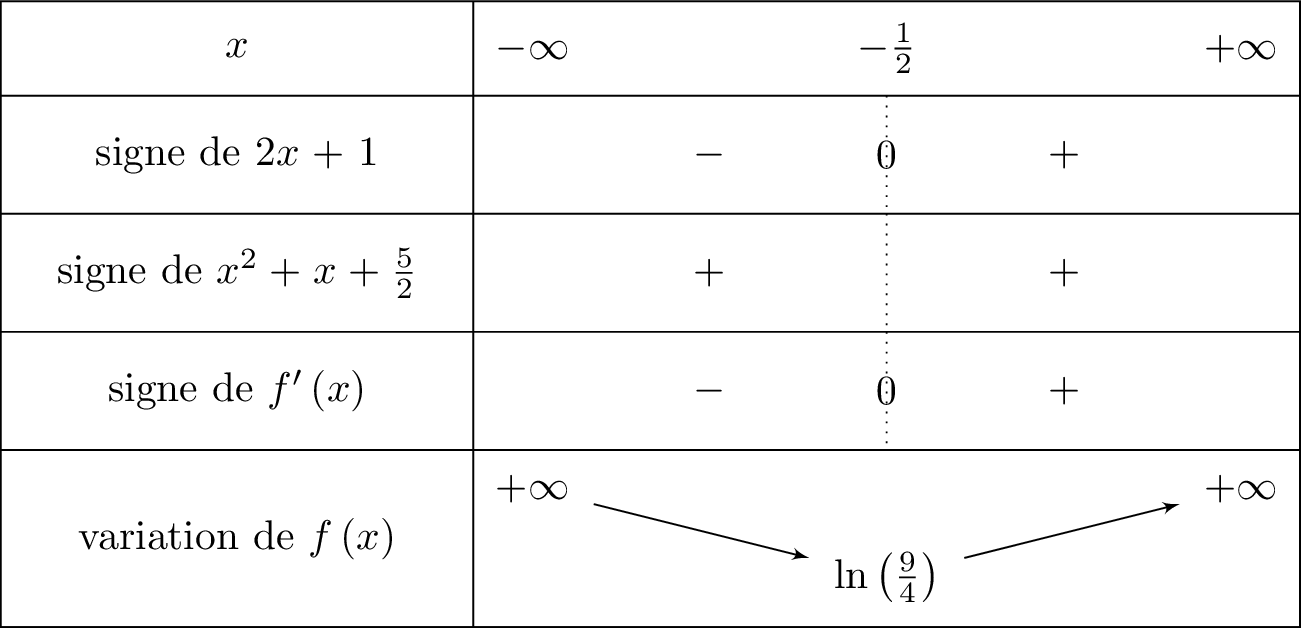
Soit
Pour tout réel , le dénominateur est strictement positif car la fonction est définie sur d'après les hypothèses initiales de la question .
Le signe de dépend alors du numérateur .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
 De plus :
De plus :
Pour tout réel , le dénominateur est strictement positif car la fonction est définie sur d'après les hypothèses initiales de la question .
Le signe de dépend alors du numérateur .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
- si alors et donc est décroissante sur cet intervalle.
- si alors et donc est croissante sur cet intervalle.

Question 8
Justifier que l’équation a une unique solution dans l’intervalle .
Correction
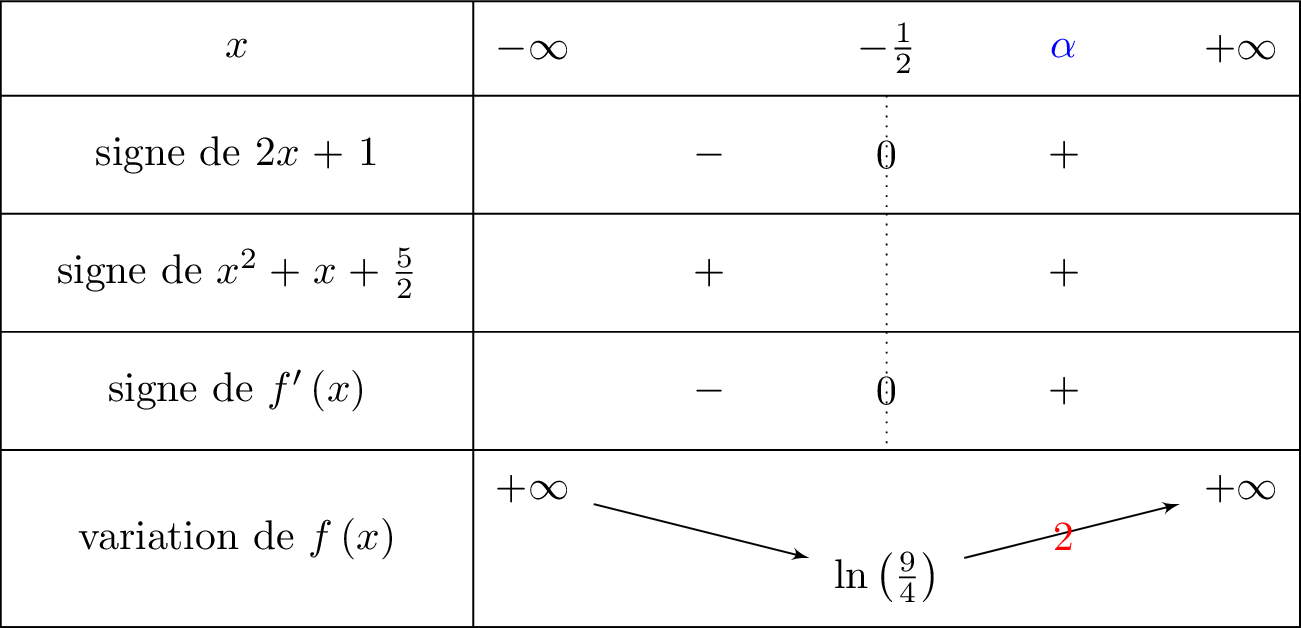
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à tel que .
Question 9
Donner une valeur approchée de à près.
Correction
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 10
La fonction est dérivable sur . On admet que, pour tout , .
Déterminer le nombre de points d'inflexion de la courbe représentative de .
Correction
D'après les hypothèses, on sait que, pour tout réel , on a : .
Nous allons étudier le signe de .
Pour tout réel , le dénominateur est strictement positif car la fonction est définie sur d'après les hypothèses initiales de la question .
Ainsi :
Le signe de dépend alors du numérateur .
C'est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de et l'étude de la convexité de .
 admet un point d'inflexion au point d'abscisse . En effet , la dérivée seconde change bien de signe en .
admet un point d'inflexion au point d'abscisse . En effet , la dérivée seconde change bien de signe en .
admet un point d'inflexion au point d'abscisse . En effet , la dérivée seconde change bien de signe en .
La courbe admet donc deux points d'inflexion.
Nous allons étudier le signe de .
Pour tout réel , le dénominateur est strictement positif car la fonction est définie sur d'après les hypothèses initiales de la question .
Ainsi :
Le signe de dépend alors du numérateur .
C'est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de signe de et l'étude de la convexité de .
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.

- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
admet un point d'inflexion au point d'abscisse . En effet , la dérivée seconde change bien de signe en .
La courbe admet donc deux points d'inflexion.