Fonction logarithme népérien
Epreuve d'enseignement de spécialité Session 13 septembre 2021 Exercice B Principaux domaines abordés : Fonction logarithme ; limites et dérivation - Exercice 1
40 min
65
Le graphique ci-dessous donne la représentation graphique dans un repère orthonormé de la fonction définie sur l’intervalle par : .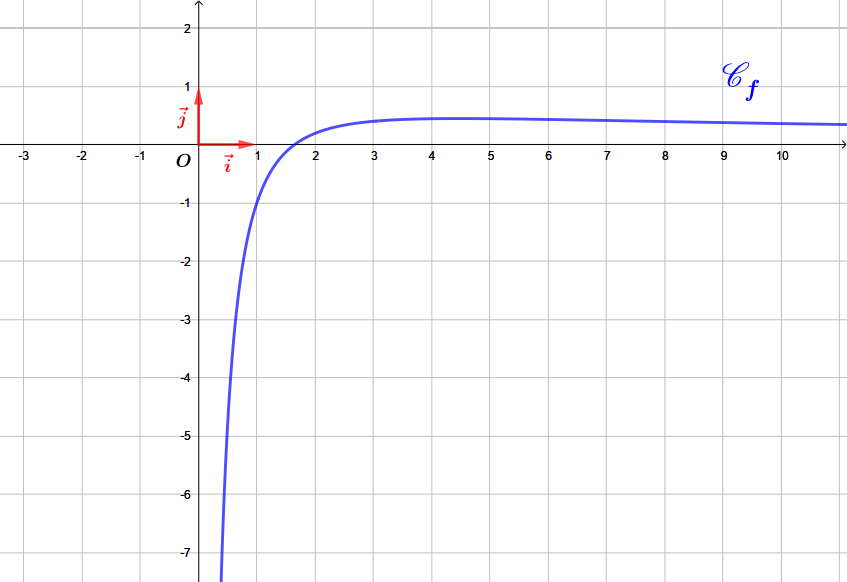

Question 1
Déterminer par le calcul l’unique solution de l’équation .
On donnera la valeur exacte de ainsi que la valeur arrondie au centième.
On donnera la valeur exacte de ainsi que la valeur arrondie au centième.
Correction
Soit .
équivaut successivement à :
et
Il faut donc résoudre
équivaut successivement à :
Ainsi :
équivaut successivement à :
et
Il faut donc résoudre
équivaut successivement à :
Ainsi :
qui correspond à la valeur exacte et
qui correspond la valeur arrondie au centième.
Question 2
Préciser, par lecture graphique, le signe de lorsque varie dans l’intervalle .
Correction
Soit .
D'après la question , nous savons que l'équation admet une unique solution .
Il vient alors que :
Si alors Si alors 
D'après la question , nous savons que l'équation admet une unique solution .
Il vient alors que :

Question 3
On considère la fonction définie sur l'intervalle par :
Déterminer la limite de la fonction en . Que peut-on en déduire?
Correction
Il en résulte que la courbe représentative de la fonction admet une d'équation .
Question 4
Déterminer la limite de la fonction en .
Correction
nous rencontrons une forme indéterminée de la forme
.
Il vient alors que :
.
Il vient alors que :
Question 5
On note la fonction dérivée de la fonction sur l’intervalle .
Démontrer que, pour tout nombre réel de , on a : , où désigne la fonction définie au début du problème.
Correction
Soit .
Ainsi :
Ainsi :
Question 6
Dresser le tableau de variations de la fonction sur l’intervalle .
On fera figurer dans ce tableau les limites de la fonction en et en , ainsi que la valeur du minimum de sur .
On fera figurer dans ce tableau les limites de la fonction en et en , ainsi que la valeur du minimum de sur .
Correction
Soit .
Nous savons que et d'après la question , on a établi que :
Si alors c'est à dire . Ainsi est décroissante sur cet intervalle. Si alors c'est à dire . Ainsi est croissante sur cet intervalle. De plus :
Ainsi :
Nous allons maintenant tout indiquer dans le tableau de variation :
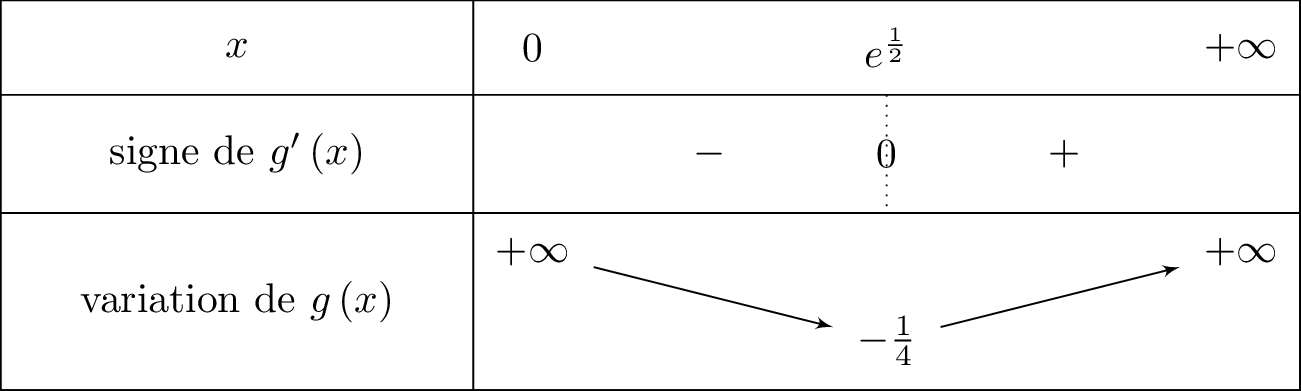
Nous savons que et d'après la question , on a établi que :
Ainsi :
Nous allons maintenant tout indiquer dans le tableau de variation :

Question 7
Démontrer que, pour tout nombre réel , l’équation admet exactement deux solutions.
Correction
La fonction admet un minimum valant lorsque
Sur , la fonction est et .
De plus, et . Soit
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Sur , la fonction est et .
De plus, et . Soit
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Il en résulte donc que l’équation admet exactement deux solutions notées et .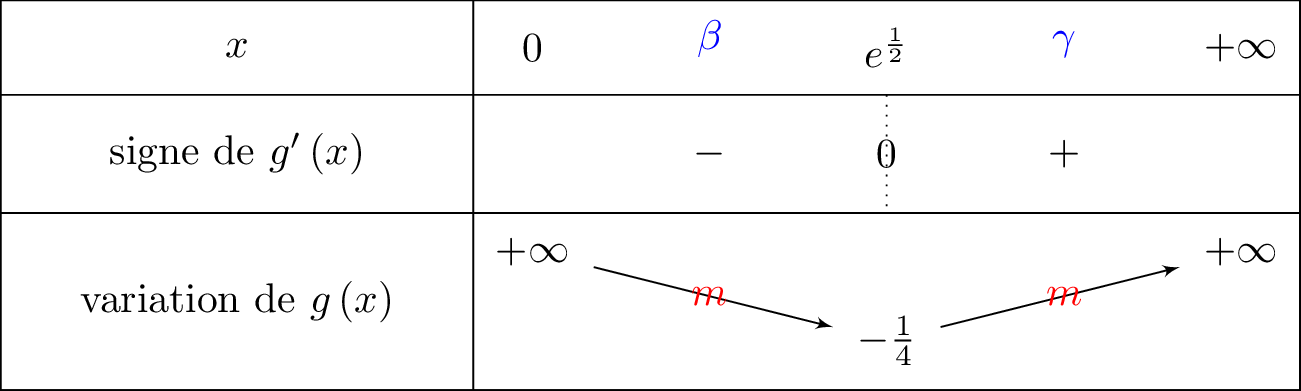
De plus, et . Soit
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
De plus, et . Soit
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à l'intervalle tel que .
Il en résulte donc que l’équation admet exactement deux solutions notées et .

Question 8
Déterminer par le calcul les deux solutions de l’équation .
Correction
équivaut successivement à :
. Nous allons factoriser par .
ou
résolvons qui donne . D'où : résolvons qui donne . D'où : Les solutions de l'équation sont alors :
. Nous allons factoriser par .
ou