Fonction logarithme népérien
Epreuve d'enseignement de spécialité Métropole Antilles-Guyane 9 septembre 2022 : fonction logarithme, suites - Exercice 1
30 min
50
On considère la fonction définie sur par : où désigne la fonction logarithme népérien.
Question 1
Déterminer la limite de quand tend vers .
Correction
- Pour tout nombre entier strictement positif, on a :
Question 2
Déterminer la limite de quand tend vers .
Correction
Soit ; nous allons factoriser par afin de pourvoir lever la forme indéterminée.
Question 3
On admet que la fonction est dérivable sur et on note sa fonction dérivée.
Démontrer que, pour tout réel , on a : .
Démontrer que, pour tout réel , on a : .
Correction
Soit . est dérivable sur .
Ici on reconnaît la forme avec ; et .
Ainsi ; et .
Il vient alors que :
Ainsi :
Ainsi ; et .
Il vient alors que :
Ainsi :
Question 4
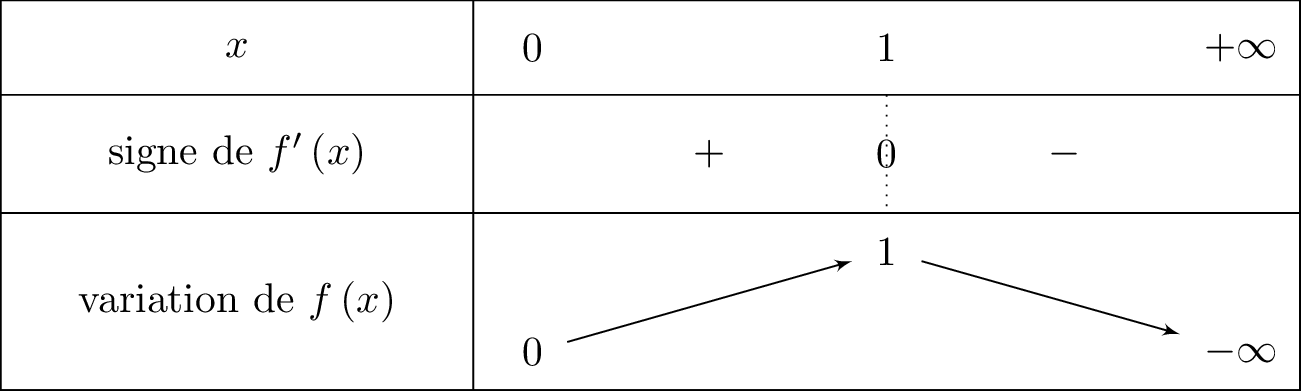
En déduire les variations de la fonction sur et dresser son tableau de variations.
Correction
Soit .
Etudions le signe de .
Il en résulte donc que :
 De plus :
De plus :
ainsi .
Etudions le signe de .
Il en résulte donc que :
- si alors donc la fonction est croissante sur cet intervalle.
- si alors donc la fonction est décroissante sur cet intervalle.

ainsi .
Question 5
Résoudre l’équation sur .
Correction
On reconnait une équation produit nul :
ou .
D'une part :
D'autre part :
N'oublions pas que nous travaillons sur l'intervalle .
il en résulte qu'il n'y a qu'une seule solution .
Ainsi :
Question 6
On considère la suite définie par : , pour tout entier naturel .
Ainsi, pour tout entier naturel , on a : .
On rappelle que la fonction est croissante sur l’intervalle .
Démontrer par récurrence que, pour tout entier naturel , on a : .
Ainsi, pour tout entier naturel , on a : .
On rappelle que la fonction est croissante sur l’intervalle .
Démontrer par récurrence que, pour tout entier naturel , on a : .
Correction
Pour tout entier naturel , posons la propriété
On sait que et ainsi .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur et donc croissante en particulier sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , .
On sait que et ainsi .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur et donc croissante en particulier sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , .
Question 7
Montrer que la suite est convergente.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 8
On note la limite de la suite . Déterminer la valeur de .
Correction
D'après le théorème du point fixe, est solution de l'équation
Or nous avons résolu cette équation à la question .
La limite de la suite est alors .
Or nous avons résolu cette équation à la question .
La limite de la suite est alors