Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Problèmes utilisant la fonction racine carré - Exercice 3
25 min
40
Question 1
La fonction est définie sur par : . On note la courbe représentative de la fonction .
Donner le signe de .
Correction
Soit :
Pour tout réel appartenant à , on a :
et .
Il en résulte donc que pour tout réel appartenant à , on a : .
Pour tout réel appartenant à , on a :
et .
Il en résulte donc que pour tout réel appartenant à , on a : .
Question 2
Déterminer la limite de en .
Correction
Si alors la fonction admet une asymptote verticale d'équation
Si alors la fonction admet une asymptote verticale d'équation
par quotient .Si alors la fonction admet une asymptote verticale d'équation
Finalement :
Interprétation graphique : la courbe admet une asymptote verticale d'équation .
Question 3
Montrer que .
Correction
Soit :
est dérivable sur .
On reconnaît la forme avec ; et
Ainsi : et et .
Il en résulte que :
équivaut successivement à :
. Il nous faut maintenant mettre tout au même dénominateur.
. Rappel :
est dérivable sur .
On reconnaît la forme avec ; et
Ainsi : et et .
Il en résulte que :
équivaut successivement à :
. Il nous faut maintenant mettre tout au même dénominateur.
. Rappel :
Question 4
En déduire le tableau de variation de la fonction . (On ne demande pas la limite de en .
Correction
Nous savons que est dérivable sur et que .
Pour tout réel appartenant à l'intervalle , le dénominateur donc le signe de dépend alors du signe de son dénominateur .
Pour étudier le signe de , nous allons utiliser le discriminant.
Comme alors le numérateur admet deux racines réelles distinctes notées et telles que :
ainsi
ainsi
, la parabole est tournée vers le haut c'est-à-dire que le numérateur est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Ainsi :
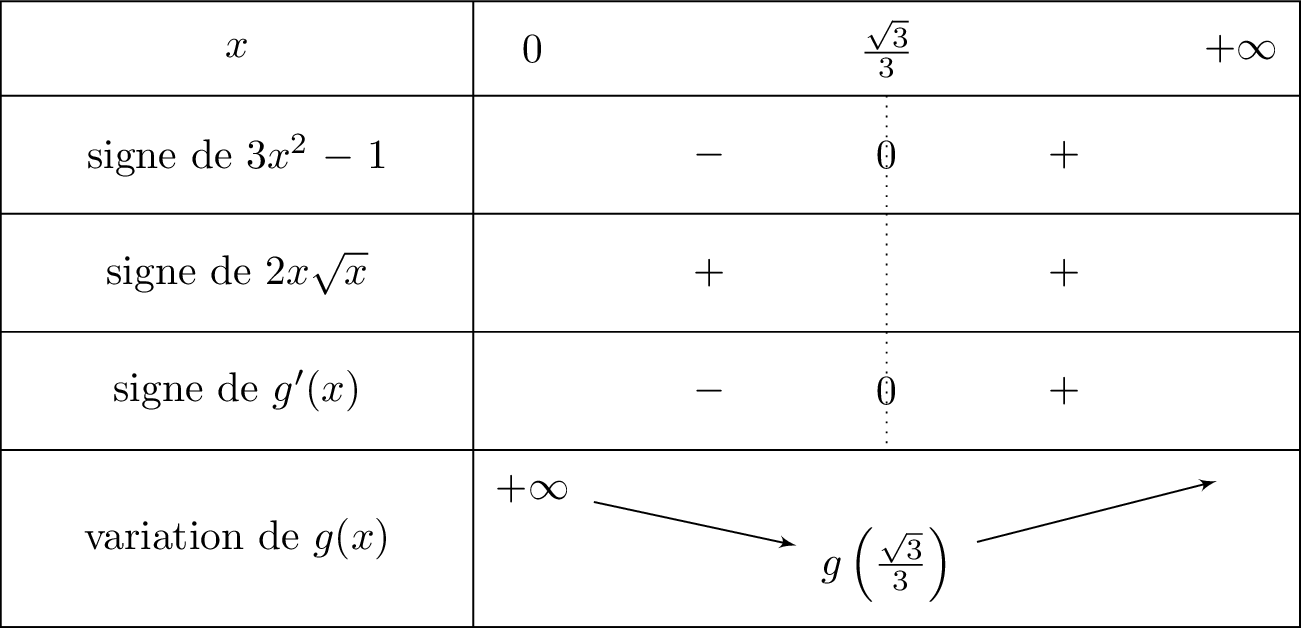
Pour tout réel appartenant à l'intervalle , le dénominateur donc le signe de dépend alors du signe de son dénominateur .
Pour étudier le signe de , nous allons utiliser le discriminant.
Comme alors le numérateur admet deux racines réelles distinctes notées et telles que :
ainsi
ainsi
, la parabole est tournée vers le haut c'est-à-dire que le numérateur est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Ainsi :

Question 5
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.