Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Problèmes utilisant la fonction racine carré - Exercice 4
10 min
25
La fonction est définie sur par : . On note la courbe représentative de la fonction .
Question 1
Pour tout réel appartenant à , calculer .
Correction
est dérivable sur .
On reconnaît la forme avec et .
Ainsi : et .
Il en résulte que :
. Nous allons tout mettre au même dénominateur .
On reconnaît la forme avec et .
Ainsi : et .
Il en résulte que :
. Nous allons tout mettre au même dénominateur .
Question 2
Dresser le tableau de variation de .
Correction
Nous savons que .
Pour tout réel appartenant à , on vérifie facilement que . Le signe de dépend alors du numérateur . Il s'agit d'un trinôme du second degré.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
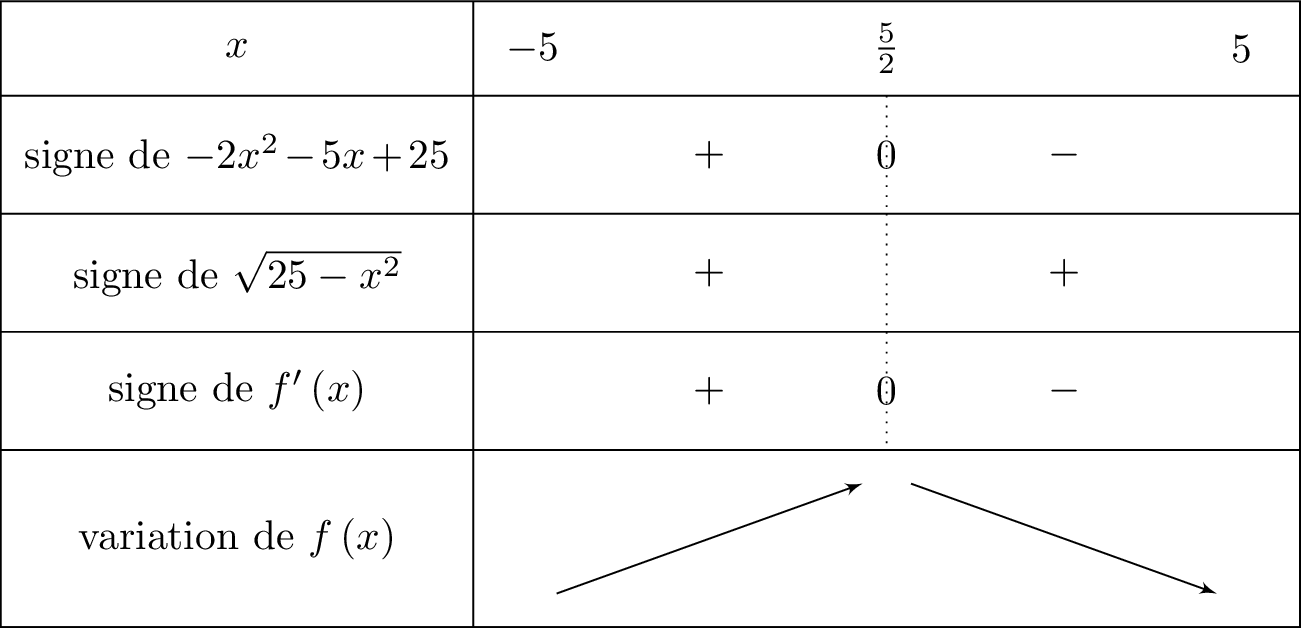
Pour tout réel appartenant à , on vérifie facilement que . Le signe de dépend alors du numérateur . Il s'agit d'un trinôme du second degré.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.