Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Problèmes utilisant la fonction racine carré - Exercice 2
30 min
50
Partie A :
La fonction est définie et dérivable sur par :
La fonction est définie et dérivable sur par :
Question 1
Déterminer la limite de en et .
Correction
D'une part :
par produit :
Finalement :
D'autre part :
par produit :
Finalement :
par produit :
Finalement :
D'autre part :
par produit :
Finalement :
Question 2
Calculer pour tout réel , étudier son signe et en déduire le tableau de variation complet de .
Correction
est dérivable sur .
On reconnaît la forme avec ; et
Ainsi : et et .
Il en résulte que :
Pour tout réel , on sait que : donc c'est à dire .
Il en résulte donc que :
et que . Il vient alors que pour tout réel on a :
Nous traduisons cela dans un tableau de variation. D'où :
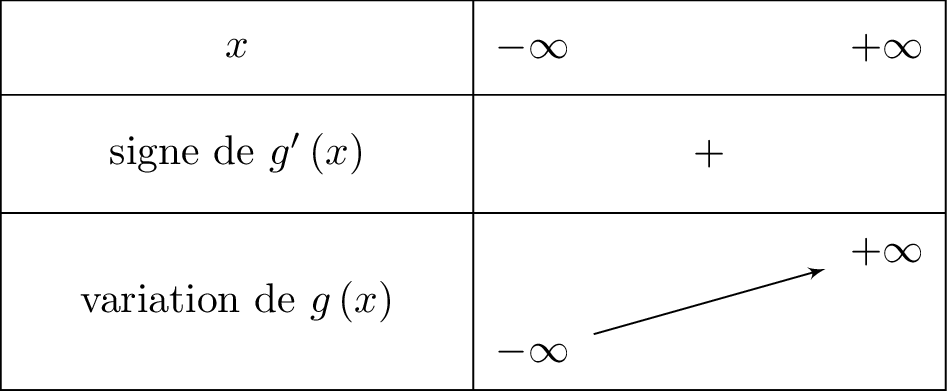
On reconnaît la forme avec ; et
Ainsi : et et .
Il en résulte que :
Pour tout réel , on sait que : donc c'est à dire .
Il en résulte donc que :
et que . Il vient alors que pour tout réel on a :
Nous traduisons cela dans un tableau de variation. D'où :

Question 3
Démontrer que l'équation admet une unique solution . Donner un encadrement de à près.
Correction
On reprend le tableau de variation fait à la question . On fera apparaître dans le tableau la valeur zéro que l'on recherche.
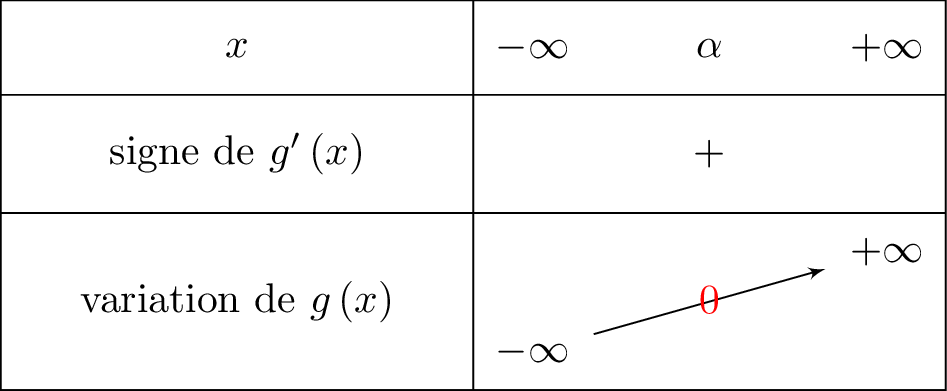
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
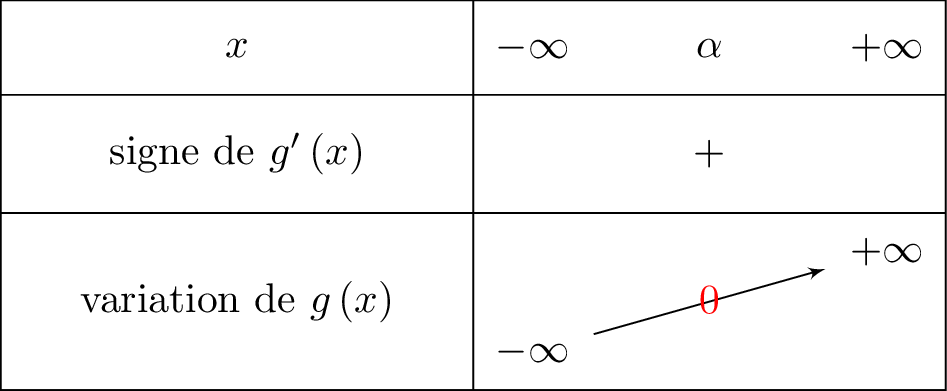
- Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à tel que .
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
Déterminer le signe de la fonction sur .
Correction
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
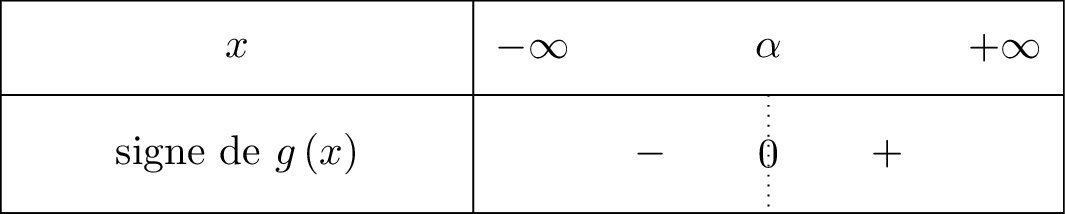
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 5
Partie B :
La fonction est définie et dérivable sur par :
La fonction est définie et dérivable sur par :
Montrer que
Correction
est dérivable sur . Il vient alors que :
. Nous allons tout mettre au même dénominateur.
. Nous factorisons maintenant le numérateur par .
Ainsi :
. Nous allons tout mettre au même dénominateur.
. Nous factorisons maintenant le numérateur par .
Ainsi :
Question 6
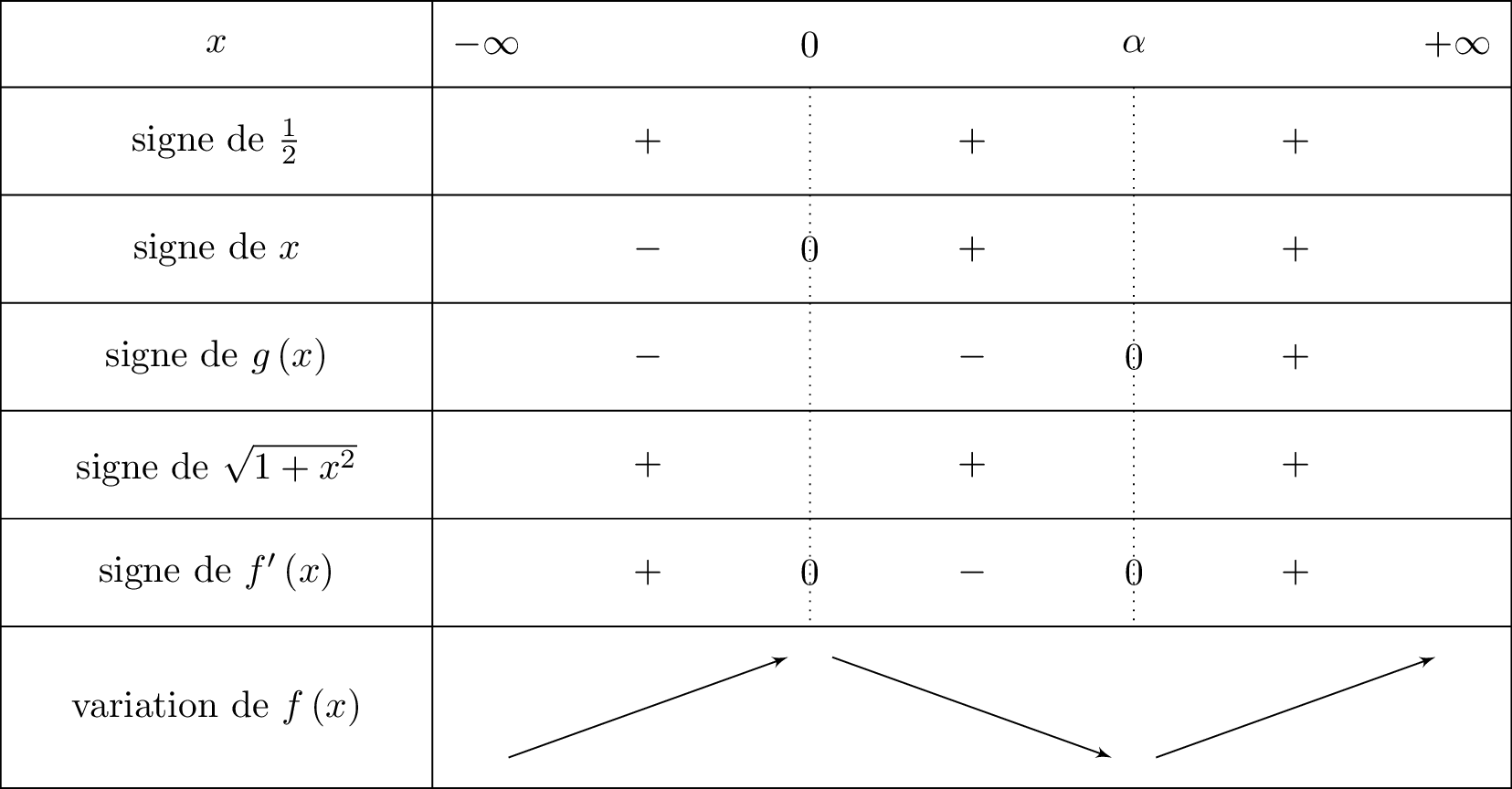
Etudier le signe de et en déduire le tableau de variation de .
Correction
Nous allons dresser le tableau de signe de . Rappelons qu'à la question de la partie A, nous avons établit le signe de .

Question 7
Montrer que
Correction
D'après la question (Partie A) on sait que : donc
Ainsi :
On a donc :
De plus :
et comme
Ainsi :
On a donc :
De plus :
et comme
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.