Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie. Applications à l'économie - Exercice 2
30 min
45
Une entreprise fabrique un produit chimique. Elle peut en produire mètres cube chaque jour ; on suppose que appartient à l'intervalle . Le coût total de production , exprimé en milliers d'euros, est fonction de la quantité produite : .
Question 1
Le prix de vente d'un mètre cube de ce produit chimique est égale à €.
On note , le bénéfice en euros réalisé par l'entreprise pour mètres cubes de produit chimique produits et vendus.
On note , le bénéfice en euros réalisé par l'entreprise pour mètres cubes de produit chimique produits et vendus.
Justifier que la fonction est continue sur l'intervalle .
Correction
est une fonction polynôme. Par définition , les fonctions polynômes sont continues sur et donc en particulier continue sur .
Question 2
Déterminer la recette , notée , correspondant à la vente de mètres cubes.
Correction
Nous savons que le prix de vente d'un mètre cube de ce produit chimique est égale à €. Il en résulte donc que pour mètres cube le prix de vente sera de .
Finalement :
Finalement :
.
Question 3
Montrer que le bénéfice, notée , est égale à : .
Correction
- Bénéfice Recette Coût de production
équivaut successivement à :
Question 4
Calculer puis vérifier que peut également s'écrire : .
Correction
est dérivable sur .
. Nous allons maintenant factoriser par .
Ainsi :
. Nous allons maintenant factoriser par .
Ainsi :
Question 5
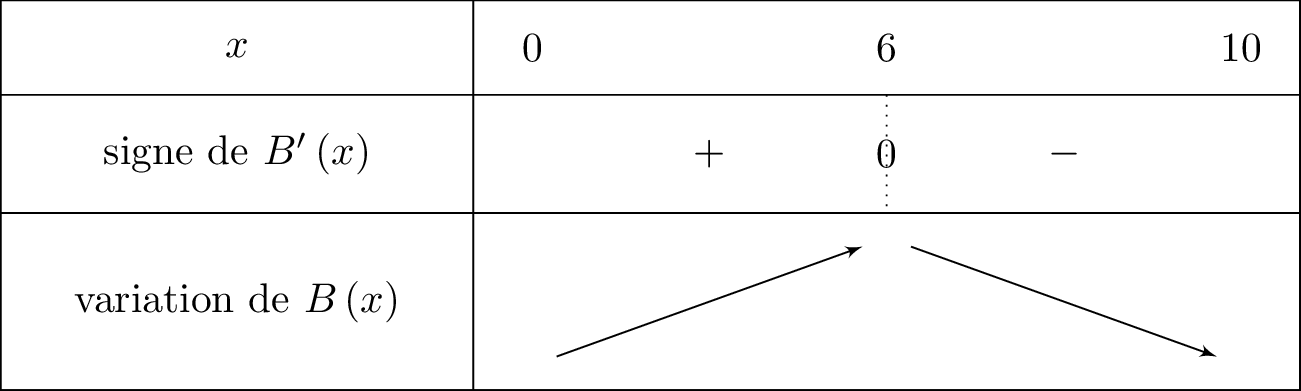
Dresser le tableau de variation complet de la fonction sur l'intervalle .
Correction
Soit . Nous savons que donc le signe de dépend de .
est une fonction trinôme du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
est une fonction trinôme du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.

Question 6
En déduire pour quelle quantité produite et vendue par jour le bénéfice réalisé par l'entreprise est maximal. Préciser la valeur de ce bénéfice maximal, en euros.
Correction
D'après la question , nous savons que :  L'entreprise devra produire et vendre mètres cube pour obtenir un bénéfice maximal. La valeur de ce bénéfice est obtenue en calculant . D'où :
L'entreprise devra produire et vendre mètres cube pour obtenir un bénéfice maximal. La valeur de ce bénéfice est obtenue en calculant . D'où :
Pour mètres cube produit et vendu, le bénéfice maximal sera de milliers d'euros.

Pour mètres cube produit et vendu, le bénéfice maximal sera de milliers d'euros.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.