Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie. Applications à l'économie - Exercice 1
20 min
35
Question 1
Une entreprise fabrique du parfum haut de Gamme. La production quotidienne varie entre et litres. Le coût total de production de litres, exprimé en milliers d’euros, est modélisée par la fonction définie sur par
Montrer que la fonction est croissante sur l'intervalle .
Correction
POur répondre à cette question nous allons donner le sens de variation de la fonction .
est dérivable sur .
On a :
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
. Donc . Il n'y a donc pas de solutions.
Comme , la parabole est tournée vers le haut c'est-à-dire que est alors du signe de . Autrement dit, sur l'intervalle , nous aurons alors .
Il vient alors que :
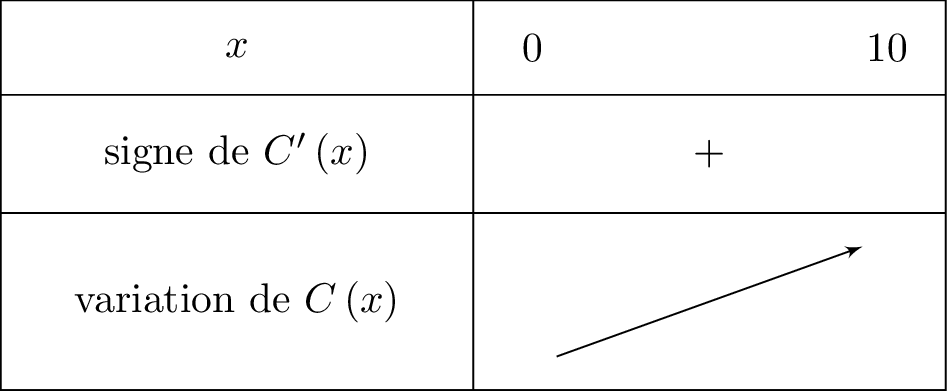
est dérivable sur .
On a :
.
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
. Donc . Il n'y a donc pas de solutions.
Comme , la parabole est tournée vers le haut c'est-à-dire que est alors du signe de . Autrement dit, sur l'intervalle , nous aurons alors .
Il vient alors que :

Question 2
Etudier la convexité de la fonction sur l'intervalle .
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de .
est dérivable sur .
Nous avons alors :
et enfin .
Ainsi :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :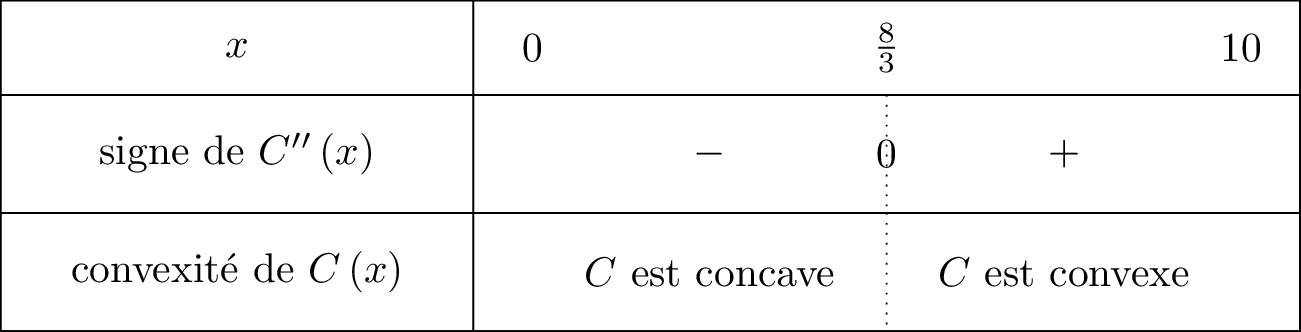
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
Nous avons alors :
et enfin .
Ainsi :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
- si alors et donc est concave sur cet intervalle.
- si alors et donc est convexe sur cet intervalle.

Question 3
Montrer que la courbe représentative de la fonction admet un point d'inflexion dont on précisera l'abscisse.
Correction
D'après la question , nous savons que : 
Il en résulte donc que et d'après le tableau ci-dessus change bien de signe lorsque .
La fonction admet un point d'inflexion dont l'abscisse .

- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
La fonction admet un point d'inflexion dont l'abscisse .
Question 4
Sur quel intervalle la croissance de est-elle ralentie? Accélérée?
Correction
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.