Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 1

15 min
25
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et justifier la réponse donnée.
Soit ff une fonction définie sur R\mathbb{R} par : f(x)=x4−6x2+5f\left(x\right)=x^{4}-6x^{2}+5 et Cf\mathscr{C_f} sa courbe représentative dans un repère du plan.
Question 1

La courbe Cf\mathscr{C_f} admet un point d'inflexion de coordonnées (1;0)\left(1;0\right).

Correction
La proposition est vraie.\red{\text{La proposition est vraie.}}
  • ff possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
Il nous faut tout d'abord calculer f′f' puis f′′f''. Il vient alors que :
Premièrement : f′(x)=4x3−12xf'\left(x\right)=4x^{3}-12x
Enfin :
f′′(x)=12x2−12f''\left(x\right)=12x^{2}-12

Résolvons :
f′′(x)=0f''\left(x\right)=0 équivaut successivement à :
12x2−12=012x^{2}-12=0. Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
Δ=576\Delta =576 , x1=−1x_{1} =-1 et x2=1x_{2} =1
Comme a=12>0a=12>0, la parabole est tournée vers le haut c'est-à-dire que f′′f'' est du signe de aa à l'extérieur des racines et du signe opposé à aa entre les racines.
Cela nous donne ci-dessous :
La dérivée seconde s'annule et change de signe en −1-1 et en 11. Donc ff admet un point d'inflexion en −1-1 et en 11.
Pour déterminer les coordonnées du point d'inflexion d'abscisse 11, il nous faut calculer f(1)f\left(1\right).
Ainsi : f(1)=14−6×12+5=0f\left(1\right)=1^{4}-6\times1^{2}+5=0.
La courbe Cf\mathscr{C_f} admet un point d'inflexion de coordonnées (1;0)\left(1;0\right).
Question 2

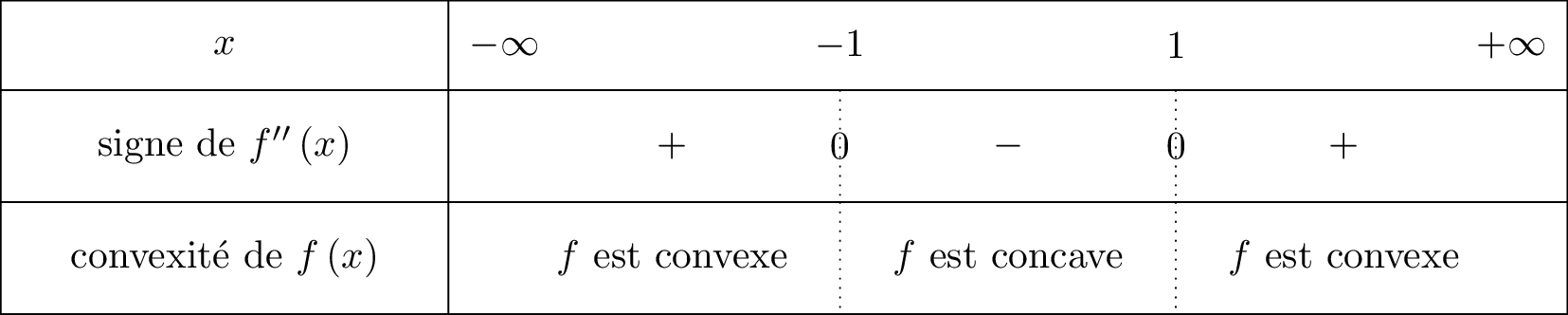
La fonction ff est convexe sur les intervalles ]−∞;−1]\left]-\infty;-1\right] et [1;+∞[\left[1;+\infty\right[. Elle est concave sur l'intervalle [−1;1]\left[-1;1\right].

Correction
La proposition est vraie.\red{\text{La proposition est vraie.}}
Nous savons que : f′′(x)=12x2−12f''\left(x\right)=12x^{2}-12 et d'après la question précédente, nous avons donné le signe de f′′f''.
  • Lorsque f′′(x)≥0f''\left(x\right)\ge 0 sur un intervalle [a,b]\left[a,b\right] alors ff est convexe.
  • Lorsque f′′(x)≤0f''\left(x\right)\le 0 sur un intervalle [a,b]\left[a,b\right] alors ff est concave.
Il vient alors que :
Question 3

La tangente TT à la courbe Cf\mathscr{C_f} au point d’abscisse −1-1 a pour équation : y=8x+16y=8x+16.

Correction
La proposition est fausse.\red{\text{La proposition est fausse.}}
L'équation de la tangente au point d'abscisse aa s'écrit y=f′(a)(x−a)+f(a)y=f'\left(a\right)\left(x-a\right)+f\left(a\right).
Ici a=−1a=-1, ce qui donne, y=f′(−1)(x−(−1))+f(−1)y=f'\left(-1\right)\left(x-\left(-1\right)\right)+f\left(-1\right). Ainsi : y=f′(−1)(x+1)+f(−1)y=f'\left(-1\right)\left(x+1\right)+f\left(-1\right)
1ère étape : calculer f(−1)f\left(-1\right)
f(−1)=(−1)4−6×(−1)2+5f\left(-1\right)=\left(-1\right)^{4}-6\times\left(-1\right)^{2}+5
f(−1)=0f\left(-1\right)=0
2ème étape : calculer f′(−1)f'\left(-1\right)
f′(−1)=4×(−1)3−12×(−1)f'\left(-1\right)=4\times\left(-1\right)^{3}-12\times\left(-1\right)
f′(−1)=8f'\left(-1\right)=8
3ème étape : on remplace les valeurs de f(−1)f\left(-1\right) et de f′(−1)f'\left(-1\right) dans la formule de l'équation de tangente.
On sait que :
y=f′(−1)(x+1)+f(−1)y=f'\left(-1\right)\left(x+1\right)+f\left(-1\right)
y=8×(x+1)y=8\times \left(x+1\right)
y=8x+8y=8x+8

Ainsi l'équation de la tangente à la courbe CfC_{f} au point d'abscisse −1-1 est alors y=8x+8y=8x+8.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.