Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Epreuve d'enseignement de spécialité Nouvelle-Calédonie 26 octobre 2022 Jour 1 - Exercice 1
30 min
50
On considère la fonction définie sur par .
On admet que la fonction est dérivable sur et on note sa fonction dérivée.
On définit la suite par et, pour tout entier naturel , .
On admet que la fonction est dérivable sur et on note sa fonction dérivée.
On définit la suite par et, pour tout entier naturel , .
Question 1
Calculer puis . On donnera les valeurs exactes, puis les valeurs approchées à .
Correction
Question 2
On considère la fonction fonc, écrite en langage Python ci-dessous.
On rappelle qu’en langage Python, « in range » signifie que varie de à .
def fonc (n)
for in range
return
Déterminer, sans justifier, la valeur renvoyée par fonc (2) arrondie à près.
On rappelle qu’en langage Python, « in range » signifie que varie de à .
def fonc (n)
for in range
return
for in range
return
Déterminer, sans justifier, la valeur renvoyée par fonc (2) arrondie à près.
Correction
D'après le rappel, en langage Python, « in range » signifie que varie de à .
Nous souhaitons la valeur renvoyée par fonc (2) .
Si l'on applique ce programme, celui ci-retournera donc la valeur de .
Nous souhaitons la valeur renvoyée par fonc (2) .
Si l'on applique ce programme, celui ci-retournera donc la valeur de .
Question 3
Calculer les limites de la fonction aux bornes de son domaine de définition.
Correction
On considère la fonction définie sur par .
D'une part :
Soit un entier naturel non nul , Il en résulte donc que
D'autre part :
De manière évidente :
D'une part :
D'autre part :
De manière évidente :
Question 4
Démontrer que, pour tout réel, on a .
Correction
On considère la fonction définie sur par .
est dérivable sur .
Ici on reconnaît la forme avec et . On a alors : et
Ainsi :
. Nous allons factoriser par .
Ainsi :
est dérivable sur .
Ainsi :
. Nous allons factoriser par .
Ainsi :
Question 5
Dresser le tableau de variation complet de la fonction .
Correction
D'après la question précédente, nous savons que pour tout réel , on a : .
Pour tout réel , on sait que : et . Le signe de dépend alors de .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :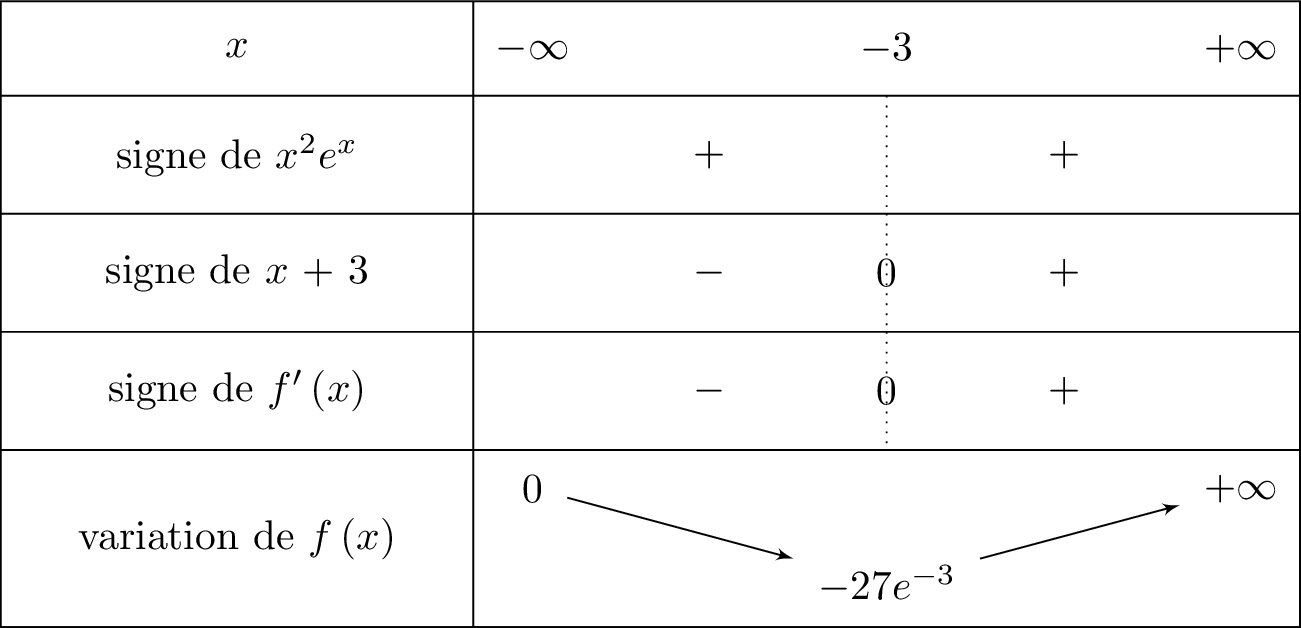 De plus :
De plus :
Pour tout réel , on sait que : et . Le signe de dépend alors de .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
- si alors et donc est décroissante sur cet intervalle.
- si alors et donc est croissante sur cet intervalle.

Question 6
Démontrer, par récurrence, que pour tout entier naturel , on a : .
Correction
Pour tout entier naturel , posons la propriété
On a vu précédemment que et .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur et donc croissante en particulier sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , .
On a vu précédemment que et .
Ainsi :
La propriété est vraie.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction croissante sur et donc croissante en particulier sur . L'ordre est donc conservé , ainsi :
. Comme alors : et . Il vient alors que :
.
De plus : et
Ainsi :
Finalement :
Ainsi la propriété est vraie.
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , .
Question 7
En déduire que la suite est convergente.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
De plus, la suite est croissante car .
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 8
On note la limite de la suite .
On rappelle que est solution de l’équation . Déterminer .
(Pour cela, on admettra que l’équation possède une seule solution dans et que celle-ci est strictement supérieure à .
On rappelle que est solution de l’équation . Déterminer .
(Pour cela, on admettra que l’équation possède une seule solution dans et que celle-ci est strictement supérieure à .
Correction
équivaut successivement à :
Il s'agit d'une équation produit nul.
D'une part :
D'autre part : . D'après le rappel, l’équation possède une seule solution dans et que celle-ci est strictement supérieure à .
D'après la question , nous savons que la suite est convergente et admet donc une limite que l'on note et comme alors .
Or une solution strictement supérieure à fait que cette solution ne peut pas appartenir à l'intervalle .
est alors la limite de la suite .
Il s'agit d'une équation produit nul.
D'une part :
D'autre part : . D'après le rappel, l’équation possède une seule solution dans et que celle-ci est strictement supérieure à .
D'après la question , nous savons que la suite est convergente et admet donc une limite que l'on note et comme alors .
Or une solution strictement supérieure à fait que cette solution ne peut pas appartenir à l'intervalle .
est alors la limite de la suite .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.