Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

De la lecture graphique à nouveau - Exercice 1

10 min
20
Cet exercice est un QCM (questionnaire à choix multiples). Pour chacune des questions posées, une seule des quatre réponses est exacte.
Pour toutes les questions de cet exercice, on considère la fonction ff définie et dérivable sur R\mathbb{R} dont la courbe représentative Cf\mathscr{C_{f}} est donnée ci-dessous.
On note f′f' la fonction dérivée de ff et f′′f'' la fonction dérivée de f′f'.
Question 1

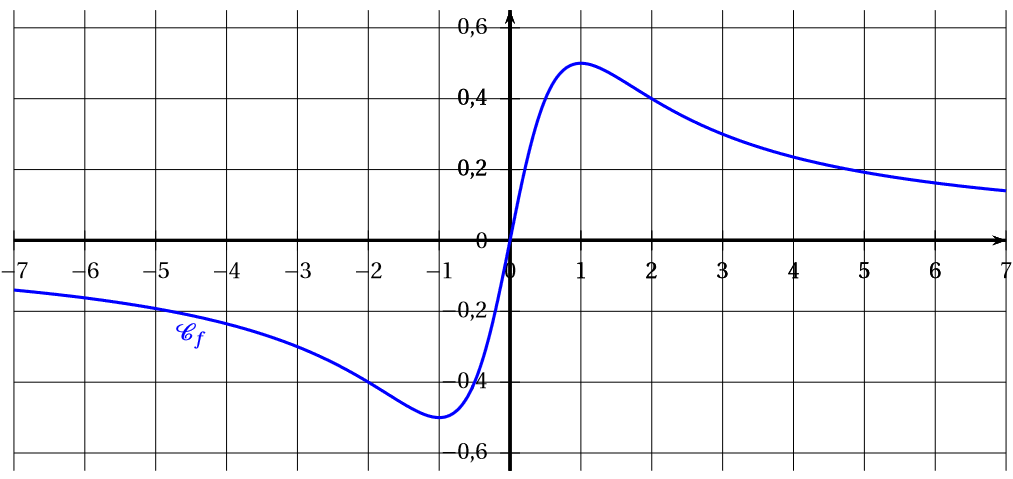
Le nombre de solutions dans [−7;7]\left[-7 ; 7\right] de l’équation f′(x)=0f'\left(x\right) = 0 est :
  • 00
  • 11
  • 22
  • 33

Correction
La bonne réponse est c .
Pour résoudre graphiquement l'équation f′(x)=0f'\left(x\right) = 0, il faut rechercher les tangentes horizontales à la courbe Cf\mathscr{C_{f}} .
Il semble qu’il existe deux tangentes horizontales à la courbe Cf\mathscr{C_{f}} sur [−7;7]\left[-7 ; 7\right] approximativement pour les points d'abscisses −1-1 et 11.
Question 2

Une valeur approchée de la solution de l’équation f(x)=−0,3f\left(x\right) =-0,3 sur l’intervalle [−1;6]\left[-1 ;6\right] est :
  • −3-3
  • −0,3-0,3
  • 0,30,3
  • 33

Correction
La bonne réponse est b .
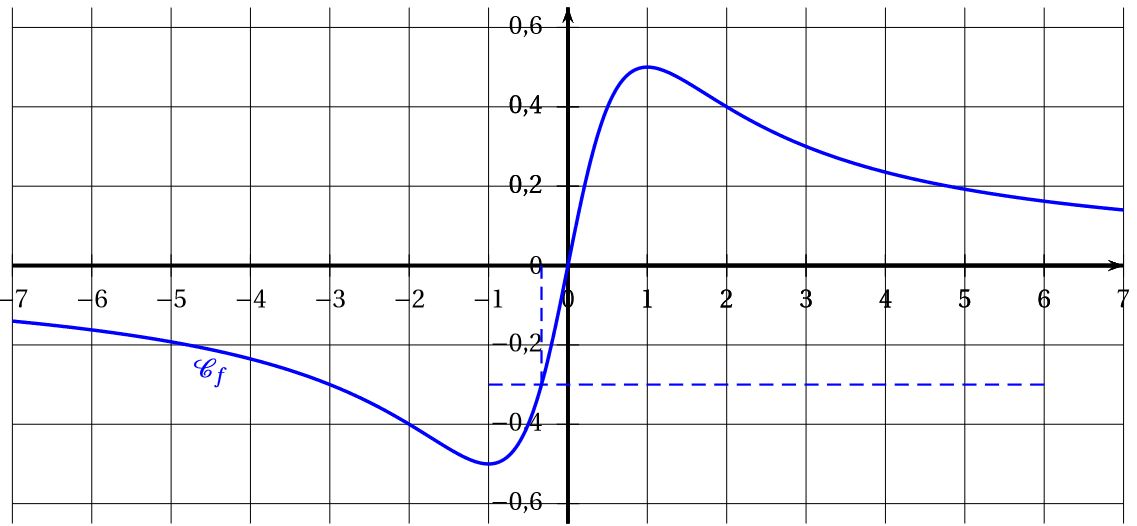
Voir les tracés en tirets en bleus sur le graphique.
Question 3

Le nombre de points d’inflexion dans [−7;7]\left[-7 ; 7\right] de Cf\mathscr{C_{f}} est :
  • 00
  • 11
  • 22
  • 33

Correction
La bonne réponse est d .
Il semble que les tangentes traversent la courbe 33 fois sur l’intervalle [−7;7]\left[-7 ; 7\right] approximativement pour les points d'abscisses −3,5-3,5 ; 00 et 22.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.