Vecteurs du plan : deuxième partie Géométrie analytique . Coordonnées des vecteurs dans une base orthonormée

Exercices Types - Exercice 2

25 min
45
Soit (0;i→;j→)\left(0;\overrightarrow{i} ;\overrightarrow{j} \right) un repère du plan. On a placé les différents points dans le graphique ci-dessous :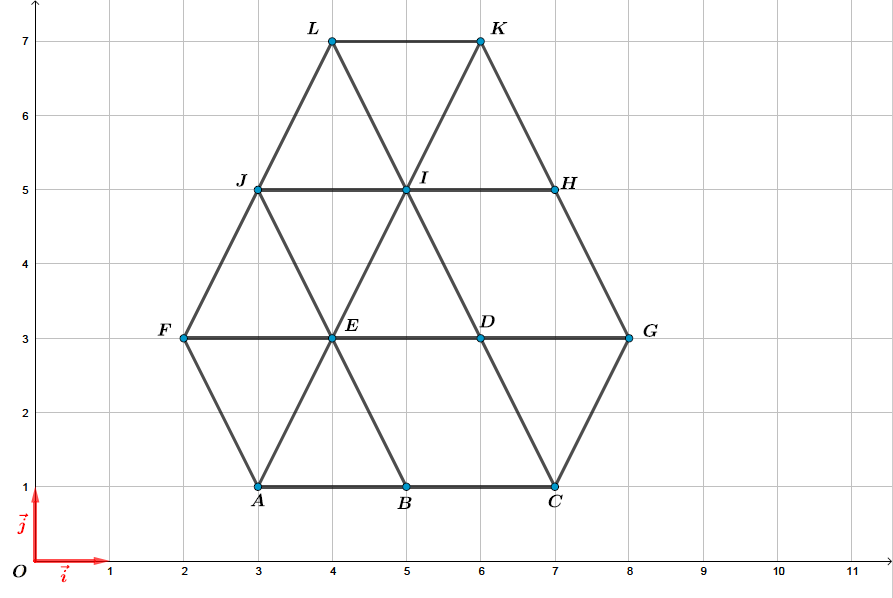
Question 1

Donner un vecteur opposé au vecteur FJ→\overrightarrow{FJ} et donner cette information en écriture mathématique.

Correction
  • Nous pouvons citer par exemple les vecteurs IE→\overrightarrow{IE} et GC→\overrightarrow{GC} ou encore EA→\overrightarrow{EA}.
    • Si nous prenons le vecteur JF⃗\vec{JF} qui est également un vecteur opposé au vecteur FJ→\overrightarrow{FJ}, alors l'écriture mathématique est la suivante :
    −FJ→=JF→-\overrightarrow{FJ}=\overrightarrow{JF}

    Question 2

    A partir de L(4;7)L\left(4;7\right) et C(7;1)C\left(7;1\right). Calculer les coordonnées du vecteur LC→\overrightarrow{LC} puis sa norme.

    Correction
  • LC→(xC−xLyC−yL)\overrightarrow{LC} \left(\begin{array}{c} {x_{C}-x_{L}} \\ {y_{C}-y_{L}} \end{array}\right) ainsi LC→(7−41−7)\overrightarrow{LC} \left(\begin{array}{c} {7-4} \\ {1-7} \end{array}\right) d'où :
    LC→(3−6)\overrightarrow{LC} \left(\begin{array}{c} {3} \\ {-6} \end{array}\right)
    • La norme du vecteur LC→\overrightarrow{LC} correspond à la distance du segment [LC]\left[LC\right]
    Soit (0;i⃗;j⃗)\left(0;\vec{i} ;\vec{j} \right) un repère orthonormal du plan et deux points A(xA;yA)A\left(x_{A} ;y_{A} \right) et B(xB;yB)B\left(x_{B} ;y_{B} \right). La distance ABAB est donnée par la formule :
    • AB=(xB−xA)2+(yB−yA)2AB=\sqrt{\left(x_{B} -x_{A} \right)^{2} +\left(y_{B} -y_{A} \right)^{2} }
    Ainsi :
    LC=(xC−xL)2+(yC−yL)2LC=\sqrt{\left(x_{C} -x_{L} \right)^{2} +\left(y_{C} -y_{L} \right)^{2} } équivaut successivement à :
    LC=(7−4)2+(1−7)2LC=\sqrt{\left(7-4 \right)^{2} +\left(1-7 \right)^{2} }
    LC=32+(−6)2LC=\sqrt{3^{2} +\left(-6\right)^{2} }
    LC=45LC=\sqrt{45 }
    LC=9×5LC=\sqrt{9\times5 }
    LC=35LC=3\sqrt{5 }
    Question 3
    Sachant que K(6;7)K\left(6;7\right) et PK→(24)\overrightarrow{PK}\left(\begin{array}{c} {2} \\ {4} \end{array}\right).

    Calculer les coordonnées du point PP. Le point PP est-il confondu avec un point de la figure? Préciser lequel?

    Correction
    Nous savons que PK→(24)\overrightarrow{PK}\left(\begin{array}{c} {2} \\ {4} \end{array}\right) et également que : PK→(xK−xPyK−yP)\overrightarrow{PK} \left(\begin{array}{c} {x_{K}-x_{P}} \\ {y_{K}-y_{P}} \end{array}\right). Finalement : PK→(6−xP7−yP)\overrightarrow{PK} \left(\begin{array}{c} {6-x_{P}} \\ {7-y_{P}} \end{array}\right)
    Il vient alors que :
    (6−xP7−yP)=(24)\left(\begin{array}{c} {6-x_{P}} \\ {7-y_{P}} \end{array}\right)=\left(\begin{array}{c} {2} \\ {4} \end{array}\right)
    On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
    {6−xP=27−yP=4\left\{\begin{array}{ccccccc} {6-x_{P}} & {=} & {2} \\ {7-y_{P}} & {=} & {4} \end{array}\right. équivaut successivement à :
    {−xP=2−6−yP=4−7\left\{\begin{array}{ccccccc} {-x_{P}} & {=} & {2-6} \\ {-y_{P}} & {=} & {4-7} \end{array}\right.
    {−xP=−4−yP=−3\left\{\begin{array}{ccccccc} {-x_{P}} & {=} & {-4} \\ {-y_{P}} & {=} & {-3} \end{array}\right.
    {xP=4yP=3\left\{\begin{array}{ccccccc} {x_{P}} & {=} & {4} \\ {y_{P}} & {=} & {3} \end{array}\right.

    Les coordonnées du point PP sont alors P(4;3)P\left(4;3\right) qui est confondu avec le point EE.
    Question 4

    Soit IQ→=BH→+AB→\overrightarrow{IQ}=\overrightarrow{BH}+\overrightarrow{AB}. Déterminer les coordonnées du point QQ.

    Correction
    D'après le repère, nous pouvons lire les coordonnées des points II, BB, HH et AA. On a alors : I(5;5)I\left(5;5\right) ; B(5;1)B\left(5;1\right) ; H(7;5)H\left(7;5\right) et A(3;1)A\left(3;1\right)
  • BH→(xH−xByH−yC)\overrightarrow{BH} \left(\begin{array}{c} {x_{H}-x_{B}} \\ {y_{H}-y_{C}} \end{array}\right) ainsi BH→(7−55−1)\overrightarrow{BH} \left(\begin{array}{c} {7-5} \\ {5-1} \end{array}\right) d'où :
    BH→(24)\overrightarrow{BH} \left(\begin{array}{c} {2} \\ {4} \end{array}\right)
  • AB→(xB−xAyB−yA)\overrightarrow{AB} \left(\begin{array}{c} {x_{B}-x_{A}} \\ {y_{B}-y_{A}} \end{array}\right) ainsi AB→(5−31−1)\overrightarrow{AB} \left(\begin{array}{c} {5-3} \\ {1-1} \end{array}\right) d'où :
    AB→(20)\overrightarrow{AB} \left(\begin{array}{c} {2} \\ {0} \end{array}\right)

    • BH→+AB→=(24)+(20)\overrightarrow{BH}+\overrightarrow{AB}= \left(\begin{array}{c} {2} \\ {4} \end{array}\right)+ \left(\begin{array}{c} {2} \\ {0} \end{array}\right)
    BH→+AB→=(44)\overrightarrow{BH}+\overrightarrow{AB}= \left(\begin{array}{c} {4} \\ {4} \end{array}\right)
  • IQ→(xQ−xIyQ−yI)\overrightarrow{IQ} \left(\begin{array}{c} {x_{Q}-x_{I}} \\ {y_{Q}-y_{I}} \end{array}\right) ainsi :
    IQ→(xQ−5yQ−5)\overrightarrow{IQ} \left(\begin{array}{c} {x_{Q}-5} \\ {y_{Q}-5} \end{array}\right)
    • Nous savons que : IQ→=BH→+AB→\overrightarrow{IQ}=\overrightarrow{BH}+\overrightarrow{AB}
    Il vient alors que :
    (xQ−5yQ−5)=(44)\left(\begin{array}{c} {x_{Q}-5} \\ {y_{Q}-5} \end{array}\right)=\left(\begin{array}{c} {4} \\ {4} \end{array}\right)
    On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
    {xQ−5=4yQ−5=4\left\{\begin{array}{ccccccc} {x_{Q}-5} & {=} & {4} \\ {y_{Q}-5} & {=} & {4} \end{array}\right. équivaut successivement à :
    {xQ=4+5yQ=5+4\left\{\begin{array}{ccccccc} {x_{Q}} & {=} & {4+5} \\ {y_{Q}} & {=} & {5+4} \end{array}\right.
    {xQ=9yQ=9\left\{\begin{array}{ccccccc} {x_{Q}} & {=} & {9} \\ {y_{Q}} & {=} & {9} \end{array}\right.
    Les coordonnées du point QQ sont Q(9;9)Q\left(9;9\right)
    Question 5

    Soit DR→=AB→−JH→\overrightarrow{DR}=\overrightarrow{AB}-\overrightarrow{JH}. Déterminer les coordonnées du point RR.

    Correction
    D'après le repère, nous pouvons lire les coordonnées des points JJ, BB, HH et AA. On a alors : J(3;5)J\left(3;5\right) ; B(5;1)B\left(5;1\right) ; H(7;5)H\left(7;5\right) et A(3;1)A\left(3;1\right)
  • JH→(xH−xJyH−yJ)\overrightarrow{JH} \left(\begin{array}{c} {x_{H}-x_{J}} \\ {y_{H}-y_{J}} \end{array}\right) ainsi JH→(7−35−5)\overrightarrow{JH} \left(\begin{array}{c} {7-3} \\ {5-5} \end{array}\right) d'où :
    JH→(40)\overrightarrow{JH} \left(\begin{array}{c} {4} \\ {0} \end{array}\right)
  • AB→(xB−xAyB−yA)\overrightarrow{AB} \left(\begin{array}{c} {x_{B}-x_{A}} \\ {y_{B}-y_{A}} \end{array}\right) ainsi AB→(5−31−1)\overrightarrow{AB} \left(\begin{array}{c} {5-3} \\ {1-1} \end{array}\right) d'où :
    AB→(20)\overrightarrow{AB} \left(\begin{array}{c} {2} \\ {0} \end{array}\right)
    • AB→−JH→=(20)−(40)\overrightarrow{AB}-\overrightarrow{JH}= \left(\begin{array}{c} {2} \\ {0} \end{array}\right)- \left(\begin{array}{c} {4} \\ {0} \end{array}\right)
    AB→−JH→=(−20)\overrightarrow{AB}-\overrightarrow{JH}= \left(\begin{array}{c} {-2} \\ {0} \end{array}\right)
  • DR→(xR−xDyR−yD)\overrightarrow{DR} \left(\begin{array}{c} {x_{R}-x_{D}} \\ {y_{R}-y_{D}} \end{array}\right) ainsi :
    DR→(xR−6yR−3)\overrightarrow{DR} \left(\begin{array}{c} {x_{R}-6} \\ {y_{R}-3} \end{array}\right)
    • Nous savons que : DR→=AB→−JH→\overrightarrow{DR}=\overrightarrow{AB}-\overrightarrow{JH}
    Il vient alors que :
    (xR−6yR−3)=(−20)\left(\begin{array}{c} {x_{R}-6} \\ {y_{R}-3} \end{array}\right)=\left(\begin{array}{c} {-2} \\ {0} \end{array}\right)
    On obtient alors deux équations à résoudre. Nous l'écrivons sous forme de système.
    {xR−6=−2yR−3=0\left\{\begin{array}{ccccccc} {x_{R}-6} & {=} & {-2} \\ {y_{R}-3} & {=} & {0} \end{array}\right. équivaut successivement à :
    {xR=−2+6yR=3\left\{\begin{array}{ccccccc} {x_{R}} & {=} & {-2+6} \\ {y_{R}} & {=} & {3} \end{array}\right.
    {xR=4yR=3\left\{\begin{array}{ccccccc} {x_{R}} & {=} & {4} \\ {y_{R}} & {=} & {3} \end{array}\right.
    Les coordonnées du point RR sont R(4;3)R\left(4;3\right)