Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercices types : 11ère partie - Exercice 1

15 min
25
Mettre une croix "x" pour indiquer que le nombre appartient à l'ensemble sinon laisser la case vide.
Question 1

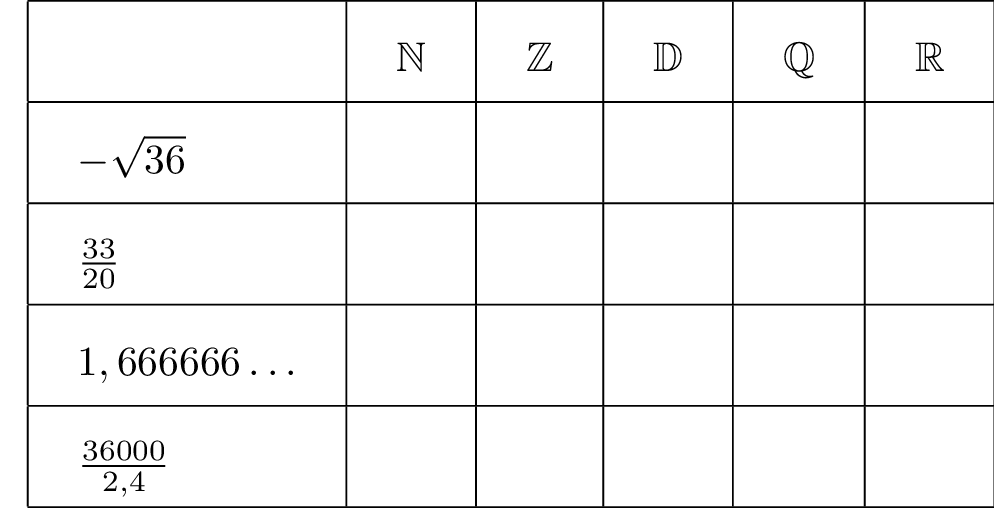
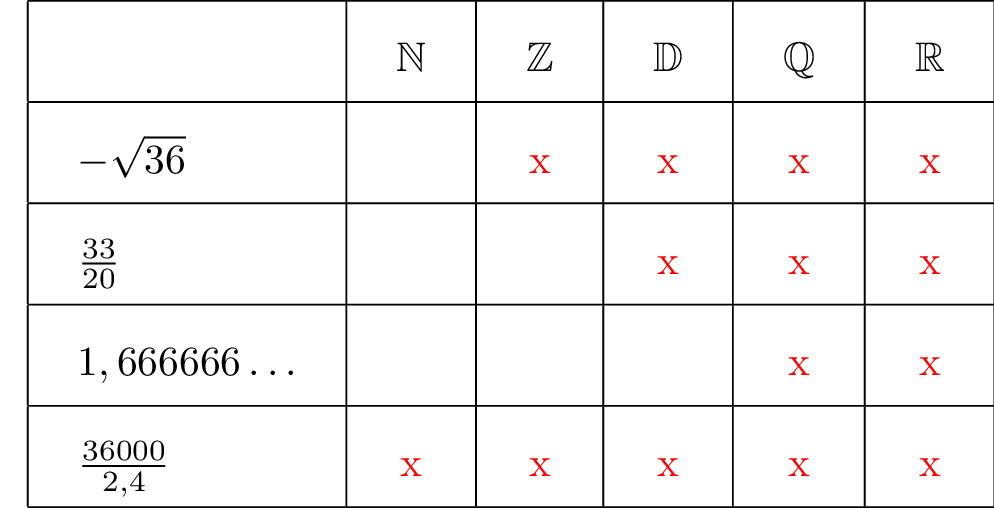
Correction
  • N={0,1,2,3,4,…}\mathbb{N}=\left\{0,1,2,3,4,\ldots \right\} est l'ensemble des entiers naturels\text{\red{entiers naturels}}. Il s'agit des entiers positifs.
  • Z={…,−3,−2,−1,0,1,2,3,4,…}\mathbb{Z}=\left\{\ldots,-3,-2,-1,0,1,2,3,4,\ldots \right\} est l'ensemble des entiers relatifs\text{\red{entiers relatifs}}. Il est composé des nombres entiers naturels et de leurs opposés.
  • L’ensemble des nombres deˊcimaux\text{\red{décimaux}} est noté D\mathbb{D}. Ce sont les nombres dont l’écriture décimale n’a qu’un nombre fini\text{\blue{fini}} de chiffres après la virgule.
  • On rappelle que Q\mathbb{Q} est l’ensemble des nombres rationnels\text{\red{rationnels}} de la forme ab\frac{a}{b} où aa est un entier relatif et bb est un entier relatif non nul.

  • −36=−6-\sqrt{36}=-6. Il en résulte donc que −6-6 est un entier relatif. Autrement dit : −6∈Z-6\in \mathbb{Z}. Comme Z⊂D⊂Q⊂R\mathbb{Z}\subset \mathbb{D}\subset \mathbb{Q}\subset \mathbb{R} alors −6∈D-6\in \mathbb{D} et également −6∈Q-6\in \mathbb{Q} et enfin −6∈R-6\in \mathbb{R}

  • 3320=1,65\frac{33}{20}=1,65. Il en résulte donc que 3320\frac{33}{20} est un nombre décimal. Autrement dit : 3320∈D\frac{33}{20}\in \mathbb{D}. Comme D⊂Q⊂R\mathbb{D}\subset \mathbb{Q}\subset \mathbb{R} alors 3320∈Q\frac{33}{20}\in \mathbb{Q} et enfin 3320∈R\frac{33}{20}\in \mathbb{R}

  • 1,666666....=531,666666....=\frac{5}{3}. Il en résulte donc que 53\frac{5}{3} n'est pas un nombre décimal mais 53\frac{5}{3} est un rationnel. Autrement dit : 53∈Q\frac{5}{3}\in \mathbb{Q}. Comme Q⊂R\mathbb{Q}\subset \mathbb{R} alors 53∈R\frac{5}{3}\in \mathbb{R}

  • 360002,4=15000\frac{36000}{2,4}=15000. Il en résulte donc que 360002,4\frac{36000}{2,4} est un entier naturel.Autrement dit : 360002,4∈N\frac{36000}{2,4}\in \mathbb{N}. Comme N⊂Z⊂D⊂Q⊂R\mathbb{N}\subset\mathbb{Z}\subset \mathbb{D}\subset \mathbb{Q}\subset \mathbb{R} alors 360002,4∈Z\frac{36000}{2,4}\in \mathbb{Z} et 360002,4∈D\frac{36000}{2,4}\in \mathbb{D} et 360002,4∈Q\frac{36000}{2,4}\in \mathbb{Q} et enfin 360002,4∈R\frac{36000}{2,4}\in \mathbb{R}
    • .
    Question 2

    Déterminer deux entiers consécutifs appartenant à l'intervalle ]−1;1]\left]-1;1\right]

    Correction
    • N={0,1,2,3,4,…}\mathbb{N}=\left\{0,1,2,3,4,\ldots \right\} est l'ensemble des entiers naturels\text{\red{entiers naturels}}. Il s'agit des entiers positifs.
    Sur l'intervalle ]−1;1]\left]-1;1\right] les deux seuls entiers consécutifs sont 00 et 11.
    Question 3

    Compléter par l'un des symboles ∈\in , ∉\notin
    10−3…[0;1[10^{-3}\ldots \left[0;1\right[

    Correction
    10−3=0,00110^{-3}=0,001. Ainsi : 0≤0,001<10\le 0,001<1
    D'où :
    10−3∈[0;1[10^{-3}\in \left[0;1\right[
    Question 4

    Compléter par l'un des symboles ∈\in , ∉\notin
    73…D\frac{7}{3}\ldots \mathbb{D}

    Correction
    • Ce sont les nombres dont l’écriture décimale n’a qu’un nombre fini de chiffres après la virgule. L’ensemble des nombres décimaux est noté D\mathbb{D}.
    Lorsque l'on tape 73\frac{7}{3} à la calculatrice on lit la valeur suivante : 2,333333333...2,333333333...
    L'écriture décimale , ici, a un nombre INFINI de chiffres après la virgule. Ainsi : 73∉D\frac{7}{3}\notin \mathbb{D}
    Question 5

    Compléter par l'un des symboles ∈\in , ∉\notin
    −2…]−2;π[-2\ldots \left]-2;\pi\right[

    Correction
    −2∉]−2;π[-2\notin \left]-2;\pi\right[
    Question 6

    Compléter par l'un des symboles ∈\in , ∉\notin
    2π…R2\pi\ldots \mathbb{R}

    Correction
    2π∈R2\pi\in \mathbb{R} car quelque soit le nombre choisi celui-ci appartiendra à l'ensemble des réels R\mathbb{R}.
    Question 7

    Compléter par l'un des symboles ∈\in , ∉\notin
    −23…Q\frac{-2}{3}\ldots \mathbb{Q}

    Correction
    • C’est l’ensemble des nombres qui s’écrivent comme le quotient d’un entier par un entier non nul. L’ensemble des nombres rationnels est noté Q\mathbb{Q}.
    −23∈Q\frac{-2}{3} \in \mathbb{Q}

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.