Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
QCM Bilan 1 - Exercice 1
2 h
165
Voici un Q.C.M. afin d'évaluer votre progression vers votre entrée dans l'enseignement supérieur.
Question 1
Cet exercice est un questionnaire à choix multiples (Q. C. M.) . Pour chacune des questions, une seule des quatre réponses est exacte.
La limite vaut :
n'existe pas
n'existe pas
Correction
Par la méthode de l'expression conjuguée, on trouve que :
Question 2
La limite vaut :
n'existe pas
n'existe pas
Correction
En effet, on a :
Ce qui nous donne en simplifiant par :
Question 3
La limite vaut :
Correction
En effet, en utilisant la définition de la dérivée en , on trouve que :
Question 4
La limite vaut :
Correction
En factorisant par dans chacune des racines carrées présentent, on trouve que :
Question 5
On considère les trois nombres réels strictement positifs , et .
La limite vaut :
La limite vaut :
Correction
En effet, on a :
On reconnait alors la définition de la dérivation en , et on obtient alors :
Question 6
Soit . L'expression de la dérivée de est :
Correction
En effet, soit . L'expression de la dérivée de est :
Question 7
Soit . L'expression de la dérivée de est :
Correction
En effet, on a :
Ce qui nous donne :
Question 8
Soit . L'expression de la dérivée de est :
Correction
En effet, on a :
Mais . Ainsi, on obtient :
Mais pour tout réel, on sait que . Finalement, on trouve que :
Question 9
Soit . L'expression de la dérivée de est :
Correction
En effet, pour , on a :
Mais comme , on a :
Question 10
On considère la fonction numérique suivante :
Cette fonction est :
dérivable à l'origine non dérivable à l'origine
discontinue à l'origne inexistante à l'origine
Cette fonction est :
dérivable à l'origine non dérivable à l'origine
discontinue à l'origne inexistante à l'origine
Correction
En effet, on a :
Or, lorsque tend vers , le terme est équivalent à . Ce qui nous permet d'écrire que :
si alors et
Dans ce cas, on a :
si alors et
Dans ce cas, on a :
On constate alors que :
Donc la fonction n'est pas dérivable à l'origine. Il y a l'existence de deux tangentes différentes au point origine.
Graphiquement, ceci se visualise très bien :
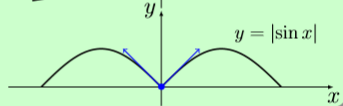
Question 11
La valeur de l'intégrale est :
Correction
En effet, on a :
Question 12
La valeur de l'intégrale est :
Correction
En effet, on a :
Or le terme est la dérivée de . Ainsi, on obtient :
Question 13
La valeur de l'intégrale est :
Correction
En effet, on a :
Or le terme est la dérivée de . Ainsi on obtient :
Question 14
La valeur de l'intégrale est :
Correction
En effet, le terme est impair sur , et l'intervalle d'intégration est symétrique par rapport à l'origine. Ainsi, en vertu de l'interprétation géométrique de l'intégrale, cette intégrale est automatiquement nulle.
Question 15
La valeur de l'intégrale est :
Correction
En effet, on a :
Ce qui nous invite à calculer la dérivée suivante :
Ainsi, on a :
Question 16
Soit un nombre réel. La solution de l'équation différentielle est de la forme :
Correction
On a une équation différentielle du premier ordre sans second membre. Donc, avec , on a :
Avec (la constante d'intégration sera prise égale à zéro) :
Donc :
Question 17
On considère les trois nombres réels , et . La solution de l'équation différentielle linéaire qui vérifie est :
Correction
la solution homogène (ou sans second membre) est avec .
la solution particulière est .
la solution mathématique est .
La condition nous donne :
Ce qui nous donne :
Question 18
Soit un nombre réel. La solution de l'équation différentielle est de la forme :
Correction
On a une équation différentielle du premier ordre sans second membre. Donc, avec , on a :
Avec (la constante d'intégration sera prise égale à zéro) :
Donc :
Question 19
Soit et deux nombres réels. La solution de l'équation différentielle est de la forme :
Correction
On pose ce qui implique que . Ainsi on obtient l'équation différentielle suivante :
Ce qui nous donne :
Donc :
En primitivant :
Posons , on obtient :
Question 20
Soit un réel. On considère l'équation différentielle . Soit et deux nombres réels, la solution de l'équation différentielle proposée est de la forme :
Correction
Il suffit de dériver deux fois la proposition et de remplacer dans l'équation différentielle proposée. On a alors :
Dans ce cas, on obtient :
Et l'équation différentielle, proposée dans cette question, est effectivement vérifiée.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.