QCM Bilan Numéro 2 - Limites de fonctions : tout ce qu'il faut retenir de la Terminale - Pré-Prépa

Question 1

Cet exercice est un questionnaire à choix multiples (QCM). Pour chacune des questions ci-dessous, une seule des réponses est exacte. Pour chaque question, vous devez bien sur justifier.

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f\left(x\right)=-x^{2}-x-1$ . La limite de $f$ en $-\infty$ est égale à :
$\bf{a.}$ $-\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $+\infty$

$\bf{c.}$ $-1$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $0$

Correction

\red{\text{La bonne réponse est}}

\red{a}

\left. \begin{array}{ccc} {\lim\limits_{x\to -\infty } -x^{2} } & {=} & {-\infty } \\ {\lim\limits_{x\to -\infty } -x-1} & {=} & {+\infty } \end{array}\right\}

nous rencontrons une forme indéterminée de la forme

+\infty -\infty

Au voisinage de

+\infty

et de

-\infty

un polynôme est équivalent à son monôme de plus haut degré.

Ce qui nous donne :

\lim\limits_{x\to -\infty } -x^{2}-x-1=\lim\limits_{x\to -\infty } -x^{2}=-\infty

\purple{\text{Finalement :}}

\lim\limits_{x\to -\infty } -x^{2}-x-1=-\infty

Question 2

Soit $f$ la fonction définie sur $\left[0;+\infty\right[$ par $f\left(x\right)=\frac{-6x^{2}+7}{2x^{2}+3}$ et $\mathscr{C_f}$ sa courbe représentative. $\mathscr{C_f}$ admet comme asymptote la droite d'équation :
$\bf{a.}$ $y=-6$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $y=0$

$\bf{c.}$ $y=-3$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $y=\frac{7}{3}$

Correction

\red{\text{La bonne réponse est}}

\red{c}

\left. \begin{array}{ccc} {\lim\limits_{x\to +\infty } -6x^{2}+7} & {=} & {-\infty } \\ {\lim\limits_{x\to +\infty } 2x^{2} +3} & {=} & {+\infty } \end{array}\right\}

on obtient une forme indéterminée

\frac{\infty }{\infty }

Au voisinage de

+\infty

et de

-\infty

un quotient de polynômes est équivalent au quotient des monômes de plus haut degré.

Il vient alors que :

{\mathop{\lim }\limits_{x\to +\infty }} \frac{-6x^{2} +7}{2x^{2} +3} ={\mathop{\lim }\limits_{x\to +\infty }} \frac{-6x^{2} }{2x^{2} } ={\mathop{\lim }\limits_{x\to +\infty }} \frac{-6 }{2 }=-3

\purple{\text{Finalement :}}

\lim\limits_{x\to +\infty } \frac{-6x^{2}+7}{2x^{2}+3} =-3

Si $\lim\limits_{x\to +\infty } f(x) =l$ où $l$ est une valeur finie alors la fonction $f$ admet une asymptote horizontale d'équation $y=l$
Si $\lim\limits_{x\to -\infty } f(x) =l$ où $l$ est une valeur finie alors la fonction $f$ admet une asymptote horizontale d'équation $y=l$

La courbe

\mathscr{C_f}

admet au voisinage de

+\infty

une asymptote horizontale d'équation

y=-3

.

Question 3

${\mathop{\lim }\limits_{x\to +\infty }} \frac{-5e^{x} }{2x^{4} } =$
$\bf{a.}$ $-\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $0$

$\bf{c.}$ $+\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $1$

Correction

\red{\text{La bonne réponse est}}

\red{a}

\red{\text{Croissance comparée}}

Pour tout entier naturel

n

non nul, on a :

\lim\limits_{x\to +\infty } \frac{e^{x}}{x^n } =+\infty

D'après le rappel, il vient que :

\lim\limits_{x\to +\infty } \frac{e^{x}}{x^4 } =+\infty

Ainsi :

{\mathop{\lim }\limits_{x\to +\infty }} \frac{-5e^{x} }{2x^{4} } ={\mathop{\lim }\limits_{x\to +\infty }} \frac{-5}{2} \times \left(\frac{e^{x} }{x^{4} } \right)=-\infty

Question 4

$\lim\limits_{x\to +\infty } \sqrt{\frac{25x+3}{x} }=$
$\bf{a.}$ $3$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $0$

$\bf{c.}$ $25$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $5$

Correction

\red{\text{La bonne réponse est}}

\red{d}

\blue{\text{Il s'agit d'une limite par composition.}}

On commence par calculer

{\mathop{\lim }\limits_{x\to +\infty }} \frac{25x+3}{x}

Au voisinage de

+\infty

et de

-\infty

un polynôme est équivalent à son monôme de plus haut degré.

Ce qui nous donne :

{\mathop{\lim }\limits_{x\to +\infty }} \frac{25x+3}{x}={\mathop{\lim }\limits_{x\to +\infty }} \frac{25x}{x}={\mathop{\lim }\limits_{x\to +\infty }} 25=25

Ainsi :

\lim\limits_{x\to {\color{red}+\infty} } \frac{25x+3}{x}={\color{blue}25}

On pose

X=\frac{25x+3}{x}

. Lorsque

x

tend vers

{\color{red}+\infty}

alors

X

tend vers

{\color{blue}25}

.
Or :

\lim\limits_{X\to {\color{blue}25}} \sqrt{X }=\sqrt{25}={\color{green}5}

Par composition :

\lim\limits_{x\to {\color{red}+\infty}} \sqrt{\frac{25x+3}{x} }={\color{green}5}

Question 5

$\lim\limits_{ \begin{array}{l} {x\to 4} \\ {x<4} \end{array} }\frac{-7x-1}{-2x+8}=$
$\bf{a.}$ $\frac{7}{2}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $+\infty$

$\bf{c.}$ $-\frac{1}{8}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $-\infty$

Correction

\red{\text{La bonne réponse est}}

\red{d}

\lim\limits_{ \begin{array}{l} {x\to 4} \\ {x<4} \end{array} }\frac{-7x-1}{-2x+8}

que l'on peut aussi écrire

\lim\limits_{x\to 4^{-} } \frac{-7x-1}{-2x+8}

\left. \begin{array}{ccc} {\lim\limits_{x\to 4^{-} } -7x-1} & {=} & {-29} \\ {\lim\limits_{x\to 4^{-} } -2x+8} & {=} & {0^{+} } \end{array}\right\}

par quotient

\lim\limits_{x\to 4^{-} } \frac{-7x-1}{-2x+8} =-\infty

.

On peut expliquer le fait que

\lim\limits_{x\to 4^{-} } -2x+8=0^{+}

de la manière suivante :
Nous avons dressé le signe de la fonction

x\mapsto -2x+8

ci dessous :

x\to 4^{-}

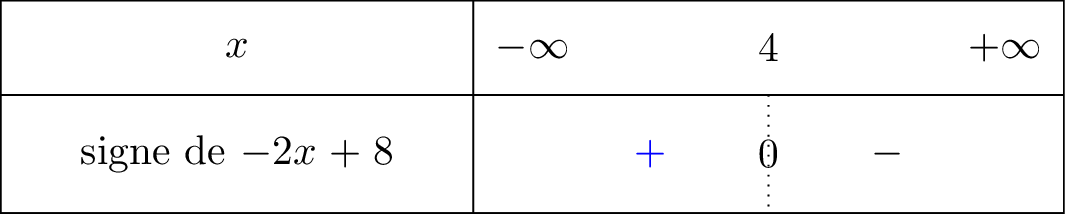signifie que

x

tend vers

4

mais avec

x<4

, donc lorsque

x<4

on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que

\lim\limits_{x\to 4^{-} } -2x+8=0^{+}

.

\frac{{\text Nombre}}{0} =\infty

, Ici on a le numérateur

-7x-1

tend vers

-29

donc négatif et le dénominateur

-2x+8

s'approche de

0

de manière positive.
Le numérateur est négatif et le dénominateur positif donc le quotient tend vers

-\infty

.

Question 6

$\lim\limits_{x\to +\infty }\frac{7+\sin \left(x\right)}{x+3}=$
$\bf{a.}$ $7$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $1$

$\bf{c.}$ $\frac{1}{3}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $0$

Correction

\red{\text{La bonne réponse est}}

\red{d}

Pour tout réel

x

, on a :

-1\le \sin \left(x\right)\le 1

équivaut successivement à :

-1+7\le 7+\sin \left(x\right)\le 7+1

6\le 7+\sin \left(x\right)\le 8

, on va ensuite diviser par

x+3

qui est strictement positif car nous sommes au voisinage de

+\infty

\frac{6}{x+3} \le \frac{7+\sin \left(x\right)}{x+3} \le \frac{8}{x+3}

\red{\text{D'une part :}}

\lim\limits_{x\to +\infty } \frac{6}{x+3} =0

\red{\text{D'autre part :}}

\lim\limits_{x\to +\infty } \frac{8}{x+3} =0

D'après le théorème des gendarmes :

\lim\limits_{x\to +\infty }\frac{7+\sin \left(x\right)}{x+3}=0

Si on rencontre une forme

\frac{Nombre}{\infty }

alors la limite sera égale à zéro.

Question 7

$\lim\limits_{x\to -\infty }\cos \left(x\right)+3x=$
$\bf{a.}$ $0$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $+\infty$

$\bf{c.}$ $-1$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $-\infty$

Correction

\red{\text{La bonne réponse est}}

\red{d}

Pour tout réel

x

, on a :

-1\le \cos \left(x\right)\le 1

équivaut successivement à :

-1+3x\le \cos \left(x\right)+3x\le 1+3x

\red{\text{D'une part :}}

\lim\limits_{x\to -\infty } -1+3x=-\infty

\red{\text{D'autre part :}}

\lim\limits_{x\to -\infty } 1+3x=-\infty

Attention, ici on n'applique pas le théorème des gendarmes car les limites ne sont pas des valeurs finies.
On va garder l'inégalité de droite, ce qui donne :

\cos \left(x\right)+3x \le 1+3x

Comme

\lim\limits_{x\to -\infty } 1+3x=-\infty

et

\cos \left(x\right)+3x \le 1+3x

alors d'après le théorème de comparaison

\lim\limits_{x\to -\infty } \cos \left(x\right)+3x=-\infty

Question 8

$\lim\limits_{ \begin{array}{l} {x\to 1} \\ {x>1} \end{array} }\frac{5x-2}{1-x^{2}}=$
$\bf{a.}$ $5$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $+\infty$

$\bf{c.}$ $2$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $-\infty$

Correction

\red{\text{La bonne réponse est}}

\red{d}

\left. \begin{array}{ccc} {\lim\limits_{x\to 1^{+} } 5x-2} & {=} & {3} \\ {\lim\limits_{x\to 1^{+} } 1-x^{2}} & {=} & {0^{-} } \end{array}\right\}

par quotient

\lim\limits_{ \begin{array}{l} {x\to 1} \\ {x>1} \end{array} }\frac{5x-2}{1-x^{2}} =-\infty

.
Interprétation graphique : la courbe admet une asymptote verticale d'équation

x=1

.

On peut expliquer le fait que

\lim\limits_{x\to 0^{-} } 1-x^{2}=0^{-}

de la manière suivante :
Nous avons dressé le signe de la fonction

x\mapsto 1-x^{2}

ci dessous :

x\to 1^{+}

signifie que

x

tend vers

1

mais avec

x>1

, donc lorsque

x>1

on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que

\lim\limits_{x\to 1^{+} } 1-x^{2}=0^{-}

.

\frac{{\text Nombre}}{0} =\infty

. Ici on a le numérateur

5x-2

tend vers

3

donc positif et le dénominateur

1-x^{2}

s'approche de

0

de manière négative.
Le numérateur est positif et le dénominateur est négatif donc le quotient tend vers

-\infty

.

Question 9

$\lim\limits_{x\to -\infty } \left(\frac{-4x^{2}-5}{x}\right)^{5} =$
$\bf{a.}$ $-\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $-4$

$\bf{c.}$ $+\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $-5$

Correction

\red{\text{La bonne réponse est}}

\red{c}

\blue{\text{Il s'agit d'une limite par composition.}}

On commence par calculer

\lim\limits_{x\to {\color{red}-\infty } }\frac{-4x^{2}-5}{x}

.
Ainsi :

\lim\limits_{x\to {\color{red}-\infty } }\frac{-4x^{2}-5}{x}=\lim\limits_{x\to {\color{red}-\infty } }\left(-\frac{4x^{2}}{x} -\frac{5}{x}\right) =\lim\limits_{x\to {\color{red}-\infty } }\left(-4x -\frac{5}{x}\right)={\color{blue}+\infty}

On pose

X=\frac{-4x^{2}-5}{x}

. Lorsque

x

tend vers

{\color{red}-\infty }

alors

X

tend vers

{\color{blue}+\infty }

.

Or :

\lim\limits_{X\to {\color{blue}+\infty}} X^{5} ={\color{green}+\infty}

Par composition :

\lim\limits_{x\to {\color{red}-\infty } } \left(\frac{-4x^{2}-5}{x}\right)^{5} ={\color{green}+\infty}

Question 10

${\mathop{\lim }\limits_{x\to +\infty }} \frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{6x^{5} +3\ln \left(x\right)-7e^{x} }=$
$\bf{a.}$ $-\frac{3}{7}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $-\infty$

$\bf{c.}$ $+\infty$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $\frac{5}{6}$

Correction

\red{\text{La bonne réponse est}}

\red{a}

\red{\text{Croissance comparée}}

Pour tout entier naturel

n

non nul, on a :

\lim\limits_{x\to +\infty } \frac{x^n}{ e^{x}} =0

\lim\limits_{x\to +\infty } \frac{\ln\left(x\right)}{e^{x}} =0

{\mathop{\lim }\limits_{x\to +\infty }} \frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{6x^{5} +3\ln \left(x\right)-7e^{x} } ={\mathop{\lim }\limits_{x\to +\infty }} \frac{e^{x} \left(\frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{e^{x} } \right)}{e^{x} \left(\frac{6x^{5} +3\ln \left(x\right)-7e^{x} }{e^{x} } \right)}

{\mathop{\lim }\limits_{x\to +\infty }} \frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{6x^{5} +3\ln \left(x\right)-7e^{x} } ={\mathop{\lim }\limits_{x\to +\infty }} \frac{e^{x} \left(\frac{5x^{5} }{e^{x} } -\frac{2\ln \left(x\right)}{e^{x} } +\frac{3e^{x} }{e^{x} } -\frac{\sqrt{x} }{e^{x} } \right)}{e^{x} \left(\frac{6x^{5} }{e^{x} } +\frac{3\ln \left(x\right)}{e^{x} } -\frac{7e^{x} }{e^{x} } \right)}

{\mathop{\lim }\limits_{x\to +\infty }} \frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{6x^{5} +3\ln \left(x\right)-7e^{x} } ={\mathop{\lim }\limits_{x\to +\infty }} \frac{\left(\frac{5x^{5} }{e^{x} } -\frac{2\ln \left(x\right)}{e^{x} } +3-\frac{\sqrt{x} }{e^{x} } \right)}{\left(\frac{6x^{5} }{e^{x} } +\frac{3\ln \left(x\right)}{e^{x} } -7\right)}

\left. \begin{array}{ccc} {\lim\limits_{x\to +\infty } \frac{5x^{5} }{e^{x} } -\frac{2\ln \left(x\right)}{e^{x} } +3-\frac{\sqrt{x} }{e^{x} } } & {=} & {3 } \\ {\lim\limits_{x\to +\infty } \frac{6x^{5} }{e^{x} } +\frac{3\ln \left(x\right)}{e^{x} } -7 } & {=} & {-7} \end{array}\right\}

\text{\red{par quotient :}}

{\mathop{\lim }\limits_{x\to +\infty }} \frac{ \left(\frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{e^{x} } \right)}{ \left(\frac{6x^{5} +3\ln \left(x\right)-7e^{x} }{e^{x} } \right)} =-\frac{3}{7}

\purple{\text{Finalement :}}

{\mathop{\lim }\limits_{x\to +\infty }} \frac{5x^{5} -2\ln \left(x\right)+3e^{x} -\sqrt{x} }{6x^{5} +3\ln \left(x\right)-7e^{x} }=-\frac{3}{7}

Question 11

${\mathop{\lim }\limits_{x\to 0}} \frac{1-e^{3x} }{7x}=$
$\bf{a.}$ $-\frac{9}{7}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $\frac{1}{7}$

$\bf{c.}$ $\frac{3}{7}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $-\frac{3}{7}$

Correction

\red{\text{La bonne réponse est}}

\red{a}

{\mathop{\lim }\limits_{x\to 0}} \frac{e^{x} -1}{x} =1

Soit

a

un réel non nul :

{\mathop{\lim }\limits_{x\to 0}} \frac{e^{ax} -1}{ax} =a

{\mathop{\lim }\limits_{x\to 0}} \frac{1-e^{3x} }{7x} ={\mathop{\lim }\limits_{x\to 0}} \left[\left(\frac{1-e^{3x} }{3x} \right)\times \frac{3}{7} \right]

{\mathop{\lim }\limits_{x\to 0}} \frac{1-e^{3x} }{7x} ={\mathop{\lim }\limits_{x\to 0}} \left[-\left(\frac{e^{3x} -1}{3x} \right)\times \frac{3}{7} \right]

{\mathop{\lim }\limits_{x\to 0}} \frac{e^{3x} -1}{3x} =3

{\mathop{\lim }\limits_{x\to 0}} \left[-\left(\frac{e^{3x} -1}{3x} \right)\times \frac{3}{7} \right]=3\times \left(-\frac{3}{7} \right)

Ainsi :

{\mathop{\lim }\limits_{x\to 0}} \left[-\left(\frac{e^{3x} -1}{3x} \right)\times \frac{3}{7} \right]=-\frac{9}{7}

QCM Bilan Numéro 2 - Exercice 1