Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Deux exercices bien sympa sur les calculs de limites quand tend vers un réel : et - Exercice 2
10 min
25
On considère la fonction
Question 1
Déterminer le domaine de définition de .
Correction
est une fonction rationnelle.
est définie pour tout réel tel que le dénominateur
Le dénominateur ici est .
est définie pour tout réel tel d'où :
L'ensemble de définition de la fonction est .
est définie pour tout réel tel que le dénominateur
Le dénominateur ici est .
est définie pour tout réel tel d'où :
L'ensemble de définition de la fonction est .
Question 2
Calculer
Correction
on obtient une forme indéterminée
Dans ce genre de situation, il faut penser à factoriser soit le numérateur soit le dénominateur .
Le dénominateur est déjà un polynôme factorisé du second degré. Le numérateur est un polynôme du second degré, nous allons le factoriser en utilisant le discriminant.
Il en résulte donc que la forme factorisée de s'écrit alors
Ainsi :
. Nous allons maintenant pouvoir simplifier le numérateur et le dénominateur par
Il vient alors que :
par quotient
Finalement :
Dans ce genre de situation, il faut penser à factoriser soit le numérateur soit le dénominateur .
Forme factorisée d'un trinôme du second degré.
Résolvons . Nous obtiendrons ; et .- Si et que nous connaissons les racines et , alors la factorisation est de la forme .
- Si et que nous connaissons la racine , alors la factorisation est de la forme .
- Si , on ne peut pas factoriser la fonction dans .
Il en résulte donc que la forme factorisée de s'écrit alors
Ainsi :
. Nous allons maintenant pouvoir simplifier le numérateur et le dénominateur par
Il vient alors que :
par quotient
Finalement :
On peut expliquer le fait que de la manière suivante :
Nous avons dressé le signe de la fonction ci dessous :
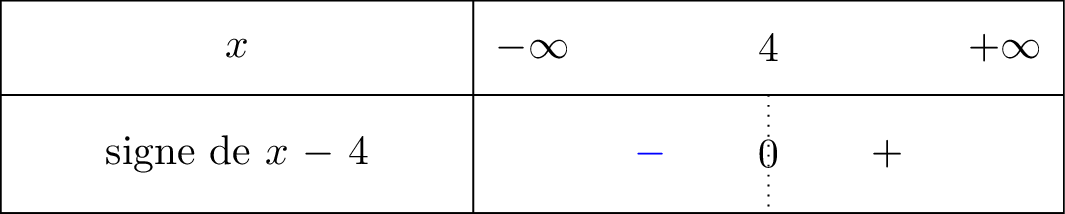 Lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que .
Lorsque on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que .
Nous avons dressé le signe de la fonction ci dessous :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.