Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Calculs de limites quand xx tend vers un réel : lim⁡x→ax<af(x){\color{blue}{\lim\limits_{ \begin{array}{l} {x\to a} \\ {x<a}\end{array}}f\left(x\right)}} et lim⁡x→ax>af(x){\color{red}{\lim\limits_{ \begin{array}{l} {x\to a} \\ {x>a} \end{array} }f\left(x\right)}} - Exercice 1

20 min
30
Calculer les limites suivantes et donner une interprétation graphique du résultat :
Question 1
Si lim⁡x→nombref(x)=+∞\lim\limits_{x\to \text{nombre}} f(x) =+\infty alors la fonction ff admet une asymptote verticale d'équation x=nombrex=\text{nombre}
Si lim⁡x→nombref(x)=−∞\lim\limits_{x\to \text{nombre}} f(x) =-\infty alors la fonction ff admet une asymptote verticale d'équation x=nombrex=\text{nombre}

lim⁡x→1+2x−1\lim\limits_{x\to 1^{+} } \frac{2}{x-1} que l'on peut aussi écrire lim⁡x→1x>12x−1\lim\limits_{ \begin{array}{l} {x\to 1} \\ {x>1} \end{array} }\frac{2}{x-1}

Correction
lim⁡x→1+2=2lim⁡x→1+x−1=0+}\left. \begin{array}{ccc} {\lim\limits_{x\to 1^{+} } 2} & {=} & {2} \\ {\lim\limits_{x\to 1^{+} } x-1} & {=} & {0^{+} } \end{array}\right\} par quotient lim⁡x→1+2x−1=+∞\lim\limits_{x\to 1^{+} } \frac{2}{x-1} =+\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=1x=1.
On peut expliquer le fait que lim⁡x→1+x−1=0+\lim\limits_{x\to 1^{+} } x-1=0^{+} de la manière suivante :
Nous avons dressé le signe de la fonction x↦x−1x\mapsto x-1 ci dessous :
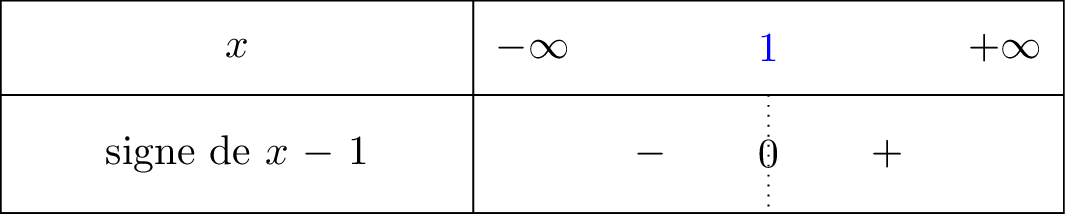x→1+x\to 1^{+} signifie que xx tend vers 11 mais avec x>1x>1, donc lorsque x>1x>1 on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que lim⁡x→1+x−1=0+\lim\limits_{x\to 1^{+} } x-1=0^{+} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur vaut 22 et il est positif et le dénominateur x−1x-1 s'approche de 00 de manière positive.
Le numérateur est positif tout comme le dénominateur donc le quotient tend vers +∞+\infty .
Question 2

lim⁡x→2−x−32x−4\lim\limits_{x\to 2^{-} } \frac{x-3}{2x-4} que l'on peut aussi écrire lim⁡x→2x<2x−32x−4\lim\limits_{ \begin{array}{l} {x\to 2} \\ {x<2} \end{array} }\frac{x-3}{2x-4}

Correction
lim⁡x→2−x−3=−1lim⁡x→2−2x−4=0−}\left. \begin{array}{ccc} {\lim\limits_{x\to 2^{-} } x-3} & {=} & {-1} \\ {\lim\limits_{x\to 2^{-} } 2x-4} & {=} & {0^{-} } \end{array}\right\} par quotient lim⁡x→2−x−32x−4=+∞\lim\limits_{x\to 2^{-} } \frac{x-3}{2x-4} =+\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=2x=2.
On peut expliquer le fait que lim⁡x→2−2x−4=0−\lim\limits_{x\to 2^{-} } 2x-4=0^{-} de la manière suivante :
Nous avons dressé le signe de la fonction x↦2x−4x\mapsto 2x-4 ci dessous :
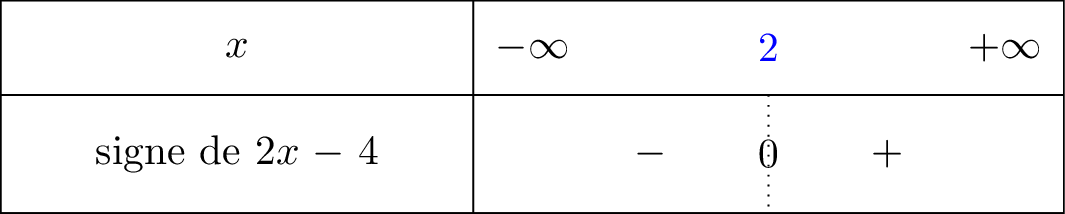x→2−x\to 2^{-} signifie que xx tend vers 22 mais avec x<2x<2, donc lorsque x<2x<2 on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que lim⁡x→2−2x−4=0−\lim\limits_{x\to 2^{-} } 2x-4=0^{-} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur x−3x-3 tend vers −1-1 donc négatif et le dénominateur 2x−42x-4 s'approche de 00 de manière négative.
Le numérateur est négatif tout comme le dénominateur donc le quotient tend vers +∞+\infty .
Question 3

lim⁡x→−3+−2x+1−x−3\lim\limits_{x\to -3^{+} } \frac{-2x+1}{-x-3} que l'on peut aussi écrire lim⁡x→−3x>−3−2x+1−x−3\lim\limits_{ \begin{array}{l} {x\to -3} \\ {x>-3} \end{array} }\frac{-2x+1}{-x-3}

Correction
lim⁡x→−3+−2x+1=7lim⁡x→−3+−x−3=0−}\left. \begin{array}{ccc} {\lim\limits_{x\to -3^{+} } -2x+1} & {=} & {7} \\ {\lim\limits_{x\to -3^{+} } -x-3} & {=} & {0^{-} } \end{array}\right\} par quotient lim⁡x→−3+−2x+1−x−3=−∞\lim\limits_{x\to -3^{+} } \frac{-2x+1}{-x-3} =-\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=−3x=-3.
On peut expliquer le fait que lim⁡x→−3+−x−3=0−\lim\limits_{x\to -3^{+} } -x-3=0^{-} de la manière suivante :
Nous avons dressé le signe de la fonction x↦−x−3x\mapsto -x-3 ci dessous :
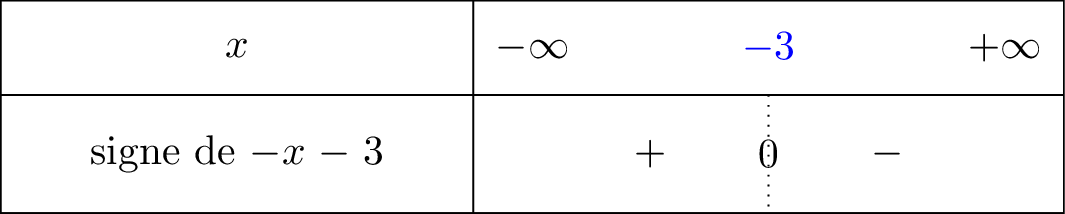x→−3+x\to -3^{+} signifie que xx tend vers −3-3 mais avec x>−3x>-3, donc lorsque x>−3x>-3 on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que lim⁡x→−3+−x−3=0−\lim\limits_{x\to -3^{+} } -x-3=0^{-} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur −2x+1-2x+1 tend vers 77 donc positif et le dénominateur −x−3-x-3 s'approche de 00 de manière négative.
Le numérateur est positif et le dénominateur est négatif donc le quotient tend vers −∞-\infty .
Question 4

lim⁡x→4−−x−x+4\lim\limits_{x\to 4^{-} } \frac{-x}{-x+4} que l'on peut aussi écrire lim⁡x→4x<4−x−x+4\lim\limits_{ \begin{array}{l} {x\to 4} \\ {x<4} \end{array} }\frac{-x}{-x+4}

Correction
lim⁡x→4−−x=−4lim⁡x→4−−x+4=0+}\left. \begin{array}{ccc} {\lim\limits_{x\to 4^{-} } -x} & {=} & {-4} \\ {\lim\limits_{x\to 4^{-} } -x+4} & {=} & {0^{+} } \end{array}\right\} par quotient lim⁡x→4−−x−x+4=−∞\lim\limits_{x\to 4^{-} } \frac{-x}{-x+4} =-\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=4x=4.
On peut expliquer le fait que lim⁡x→4−−x+4=0+\lim\limits_{x\to 4^{-} } -x+4=0^{+} de la manière suivante :
Nous avons dressé le signe de la fonction x↦−x+4x\mapsto -x+4 ci dessous :
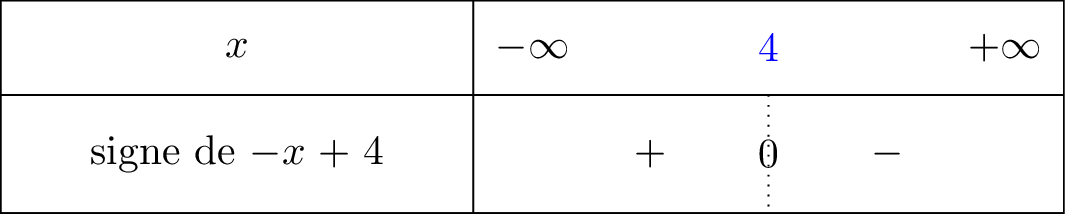x→4−x\to 4^{-} signifie que xx tend vers 44 mais avec x<4x<4, donc lorsque x<4x<4 on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que lim⁡x→4−−x+4=0+\lim\limits_{x\to 4^{-} } -x+4=0^{+} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur −x-x tend vers −4-4 donc négatif et le dénominateur −x+4-x+4 s'approche de 00 de manière positive.
Le numérateur est négatif et le dénominateur est positif donc le quotient tend vers −∞-\infty .
Question 5

lim⁡x→2−−33x−6\lim\limits_{x\to 2^{-} } \frac{-3}{3x-6} que l'on peut aussi écrire lim⁡x→2x<2−33x−6\lim\limits_{ \begin{array}{l} {x\to 2} \\ {x<2} \end{array} }\frac{-3}{3x-6}

Correction
lim⁡x→2−−3=−3lim⁡x→2−3x−6=0−}\left. \begin{array}{ccc} {\lim\limits_{x\to 2^{-} } -3} & {=} & {-3} \\ {\lim\limits_{x\to 2^{-} } 3x-6} & {=} & {0^{-} } \end{array}\right\} par quotient lim⁡x→2−−33x−6=+∞\lim\limits_{x\to 2^{-} } \frac{-3}{3x-6} =+\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=2x=2.
On peut expliquer le fait que lim⁡x→2−3x−6=0−\lim\limits_{x\to 2^{-} } 3x-6=0^{-} de la manière suivante :
Nous avons dressé le signe de la fonction x↦3x−6x\mapsto 3x-6 ci dessous :
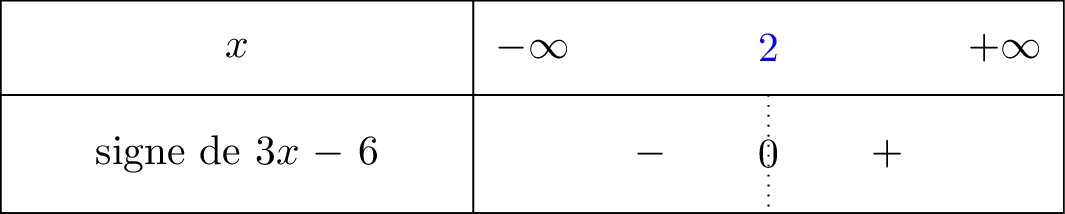x→2−x\to 2^{-} signifie que xx tend vers 22 mais avec x<2x<2, donc lorsque x<2x<2 on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que lim⁡x→2−3x−6=0−\lim\limits_{x\to 2^{-} } 3x-6=0^{-} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur tend vers −3-3 et il est négatif et le dénominateur 3x−63x-6 s'approche de 00 de manière négative donc le quotient tend vers +∞+\infty .
Question 6

lim⁡x→5−−2x(x−5)2\lim\limits_{x\to 5^{-} }\frac{-2x}{\left(x-5\right)^{2} } que l'on peut aussi écrire lim⁡x→5x<5−2x(x−5)2\lim\limits_{ \begin{array}{l} {x\to 5} \\ {x<5} \end{array} }\frac{-2x}{\left(x-5\right)^{2} }

Correction
lim⁡x→5−−2x=−10lim⁡x→5−(x−5)2=0+}\left. \begin{array}{ccc} {\lim\limits_{x\to 5^{-} } -2x} & {=} & {-10} \\ {\lim\limits_{x\to 5^{-} } \left(x-5\right)^{2}} & {=} & {0^{+} } \end{array}\right\} par quotient lim⁡x→5−−2x(x−5)2=−∞\lim\limits_{x\to 5^{-} }\frac{-2x}{\left(x-5\right)^{2} } =-\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=5x=5.
On peut expliquer le fait que lim⁡x→5−(x−5)2=0+\lim\limits_{x\to 5^{-} } \left(x-5\right)^{2}=0^{+} de la manière suivante :
Nous avons dressé le signe de la fonction 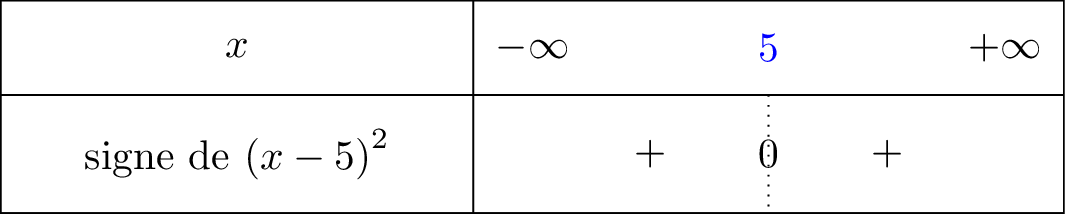x↦(x−5)2x\mapsto \left(x-5\right)^{2} ci dessous :
x→5−x\to 5^{-} signifie que xx tend vers 55 mais avec x<5x<5, donc lorsque x<5x<5 on voit bien à l'aide du tableau de signe que nous sommes dans la partie positive. C'est pour cela que lim⁡x→5−(x−5)2=0+\lim\limits_{x\to 5^{-} } \left(x-5\right)^{2}=0^{+} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur tend vers −10-10 et il est négatif et le dénominateur 3x−63x-6 s'approche de 00 de manière positive donc le quotient tend vers −∞-\infty .
Question 7

lim⁡x→5+2x+1−x+5\lim\limits_{x\to 5^{+} } \frac{2x+1}{-x+5} que l'on peut aussi écrire lim⁡x→5x>52x+1−x+5\lim\limits_{ \begin{array}{l} {x\to 5} \\ {x>5} \end{array} }\frac{2x+1}{-x+5}

Correction
lim⁡x→5+2x+1=11lim⁡x→5+−x+5=0−}\left. \begin{array}{ccc} {\lim\limits_{x\to 5^{+} } 2x+1} & {=} & {11} \\ {\lim\limits_{x\to 5^{+} } -x+5} & {=} & {0^{-} } \end{array}\right\} par quotient lim⁡x→5+2x+1−x+5=−∞\lim\limits_{x\to 5^{+} } \frac{2x+1}{-x+5} =-\infty .
Interprétation graphique : la courbe admet une asymptote verticale d'équation x=5x=5.
On peut expliquer le fait que lim⁡x→5+−x+5=0−\lim\limits_{x\to 5^{+} } -x+5=0^{-} de la manière suivante :
Nous avons dressé le signe de la fonction x↦−x+5x\mapsto -x+5 ci dessous :
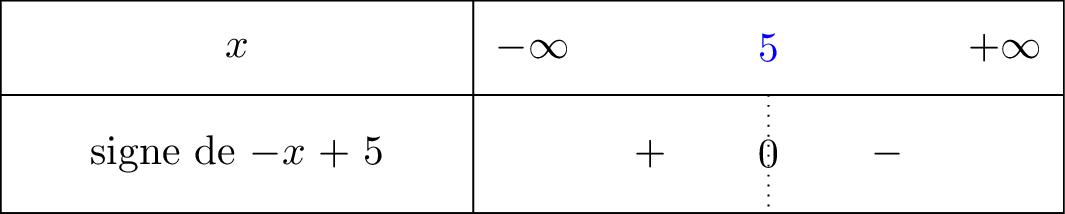x→5+x\to 5^{+} signifie que xx tend vers 55 mais avec x>5x>5, donc lorsque x>5x>5 on voit bien à l'aide du tableau de signe que nous sommes dans la partie négative. C'est pour cela que lim⁡x→5+−x+5=0−\lim\limits_{x\to 5^{+} } -x+5=0^{-} .
Nombre0=∞\frac{{\text Nombre}}{0} =\infty , Ici on a le numérateur 2x+12x+1 tend vers 1111 donc positif et le dénominateur −x+5-x+5 s'approche de 00 de manière négative.
Le numérateur est positif et le dénominateur est négatif donc le quotient tend vers −∞-\infty .

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.