Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Intégration par parties (I.P.P.) - Exercice 1
40 min
60
La méthode de l’intégration par parties est une méthode, très pratique et très puissante, qui permet d’intégrer des fonctions dont la détermination des primitives n’est pas directe. Cette méthode se prête parfaitement à des fonctions numériques à intégrer de la forme produit : .
On considère alors deux fonctions numériques, et , ne dépendant que de la variable , qui sont bornées et au moins dérivable une fois (donc continues) sur l'intervalle . Dans ce cas, , on a :
Soit :
En intégrant cette relation sur l'intervalle , on obtient alors :
En faisant usage de la linéarité de l'intégrale, on obtient alors :
Or, le deuxième terme est très facile à calculer. En effet, on a :
Par simplicité d'écriture, on écrit :
Ce qui signifie que lors du processus d'intégration par partie d'une fonction produit, il est possible de considérer les deux fonctions participantes comme :
l'une, , déjà dérivée de sa primitive. Elle "donnera naissance" à par intégration ;
l'autre, , comme primitive, donc à dérivée. Elle "donnera naissance" à par dérivation.
Ainsi, on a :
Technique de calcul d'une intégrale : l'intégration par parties
Soient deux fonctions numériques, et , ne dépendant que de la variable , qui sont bornées et au moins dérivable une fois (donc continues) sur l'intervalle . Dans ce cas, , on a la formule suivante :
Il s'agit surtout d'une méthode qui exprime différemment une intégrale, et à pour but d'en faire apparaître une plus simple à calculer.
D'un point de vue pratique, on peut procéder ainsi : en constatant que la dérivation d'un polynôme diminue son degré, et qu'à l'inverse, son intégration augmente son degré, nous symboliserons l'opération de dérivation par la flèche , alors que l'intégration sera symbolisée par la flèche . On a alors la séquence représentative suivante :
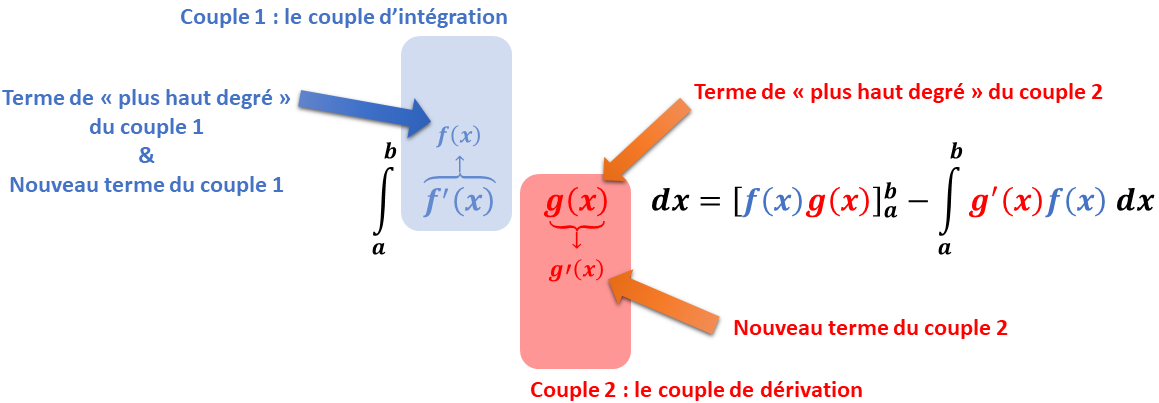
On peut alors considérer l'apparition des deux "couples" et et chacun de ces deux couples est constitué :
d'un terme initialement présent dans l'intégrale initiale : {\color{blue}{}} et ;
et d'un nouveau terme qui est apparu, l'un par intégration , et l'autre par dérivation .
De plus, on dit que :
dans le premier couple , le terme est le terme "de plus haut degré" ;
dans le second couple , le terme est le terme "de plus haut degré".
Dès lors, on applique la règle pratique suivante :
Pour le calcul d'une intégrale :
On effectue une multiplication toute intégrée des termes de plus haut degré, moins l'intégrale des deux nouveaux termes.
Pour le calcul d'une primitive :
On effectue une multiplication toute primitivée des termes de plus haut degré, moins la primitive des deux nouveaux termes.
Dans cette méthode de l'intégration par parties, il ne faut pas se tromper sur le choix de la fonction initialement à dériver et celle à intégrer. Sinon, le calcul du dernier terme peut se révéler plus délicat. Parfois, il arrive même que ce dernier terme à calculer, doive lui-même subir une autre intégration par parties. Vous devez donc toujours envisager l'expression de ce dernier terme afin qu'il soit plus aisé à calculer que l'intégrale initiale. C'est pourquoi, il est conseiller de :
dériver les termes du type ;
dériver les termes du type ;
intégrer les termes du type et ;
intégrer les termes du type ;
intégrer les termes du type si un terme en logarithme est présent.
On considère alors deux fonctions numériques, et , ne dépendant que de la variable , qui sont bornées et au moins dérivable une fois (donc continues) sur l'intervalle . Dans ce cas, , on a :
Soit :
En intégrant cette relation sur l'intervalle , on obtient alors :
En faisant usage de la linéarité de l'intégrale, on obtient alors :
Or, le deuxième terme est très facile à calculer. En effet, on a :
Par simplicité d'écriture, on écrit :
Ce qui signifie que lors du processus d'intégration par partie d'une fonction produit, il est possible de considérer les deux fonctions participantes comme :
l'une, , déjà dérivée de sa primitive. Elle "donnera naissance" à par intégration ;
l'autre, , comme primitive, donc à dérivée. Elle "donnera naissance" à par dérivation.
Ainsi, on a :
Technique de calcul d'une intégrale : l'intégration par parties
Soient deux fonctions numériques, et , ne dépendant que de la variable , qui sont bornées et au moins dérivable une fois (donc continues) sur l'intervalle . Dans ce cas, , on a la formule suivante :
Il s'agit surtout d'une méthode qui exprime différemment une intégrale, et à pour but d'en faire apparaître une plus simple à calculer.
D'un point de vue pratique, on peut procéder ainsi : en constatant que la dérivation d'un polynôme diminue son degré, et qu'à l'inverse, son intégration augmente son degré, nous symboliserons l'opération de dérivation par la flèche , alors que l'intégration sera symbolisée par la flèche . On a alors la séquence représentative suivante :

On peut alors considérer l'apparition des deux "couples" et et chacun de ces deux couples est constitué :
d'un terme initialement présent dans l'intégrale initiale : {\color{blue}{}} et ;
et d'un nouveau terme qui est apparu, l'un par intégration , et l'autre par dérivation .
De plus, on dit que :
dans le premier couple , le terme est le terme "de plus haut degré" ;
dans le second couple , le terme est le terme "de plus haut degré".
Dès lors, on applique la règle pratique suivante :
Pour le calcul d'une intégrale :
On effectue une multiplication toute intégrée des termes de plus haut degré, moins l'intégrale des deux nouveaux termes.
Pour le calcul d'une primitive :
On effectue une multiplication toute primitivée des termes de plus haut degré, moins la primitive des deux nouveaux termes.
Dans cette méthode de l'intégration par parties, il ne faut pas se tromper sur le choix de la fonction initialement à dériver et celle à intégrer. Sinon, le calcul du dernier terme peut se révéler plus délicat. Parfois, il arrive même que ce dernier terme à calculer, doive lui-même subir une autre intégration par parties. Vous devez donc toujours envisager l'expression de ce dernier terme afin qu'il soit plus aisé à calculer que l'intégrale initiale. C'est pourquoi, il est conseiller de :
dériver les termes du type ;
dériver les termes du type ;
intégrer les termes du type et ;
intégrer les termes du type ;
intégrer les termes du type si un terme en logarithme est présent.
Question 1
A l'aide de l'intégration par parties(I.P.P.), calculer les intégrales suivantes :
Correction
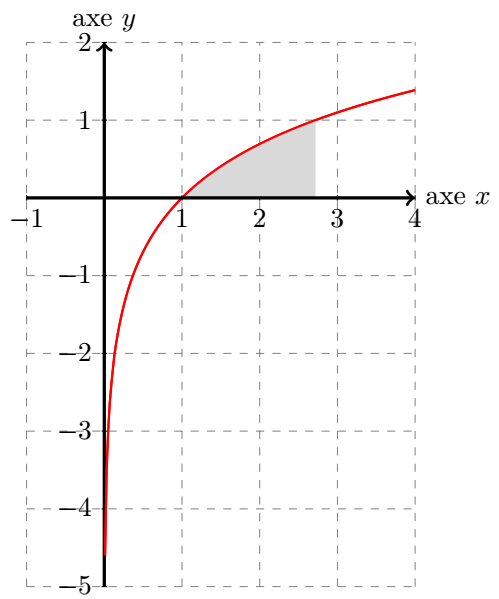
Sur l'intervalle d'intégration , le terme est strictement positif. Donc , ce qui implique :
On a alors la séquence d'intégration suivante :
Soit :
Soit encore :
Finalement, on obtient :
Graphiquement, on a :
On a alors la séquence d'intégration suivante :
Soit :
Soit encore :
Finalement, on obtient :
Graphiquement, on a :

Question 2
En déduire une primitive de
Correction
Notons par une primitive du terme .
D'après la question précédente, on peut écrire que :
Soit le résultat important suivant :
avec .
D'après la question précédente, on peut écrire que :
Soit le résultat important suivant :
avec .
Question 3
Correction
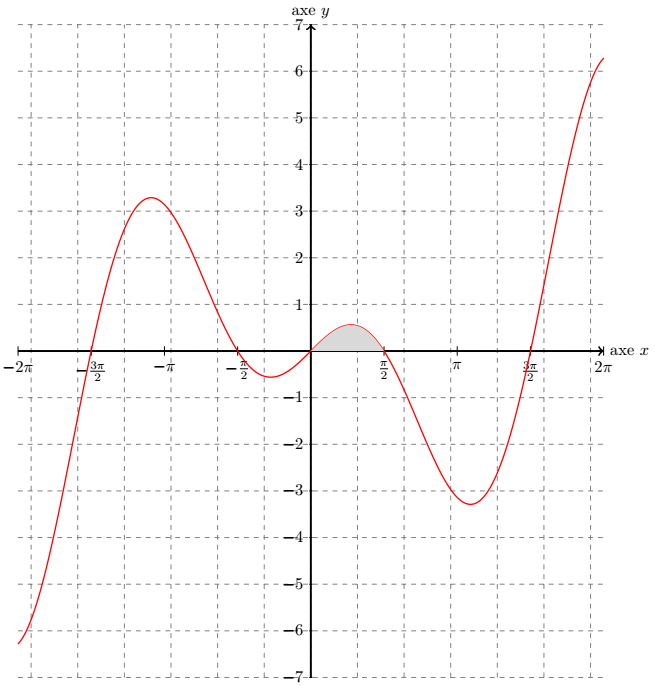
On cherche à calculer l'intégrale suivante :
On a la séquence d'intégration suivante :
Soit :
Soit encore :
Ainsi, on obtient :
Finalement, on obtient :
Graphiquement, on obtient :
On a la séquence d'intégration suivante :
Soit :
Soit encore :
Ainsi, on obtient :
Finalement, on obtient :
Graphiquement, on obtient :

Question 4
Correction
On cherche à calculer l'intégrale suivante :
Sur l'intervalle d'intégration , le terme est strictement positif. Donc , ce qui implique :
On a alors la séquence d'intégration suivante :
Ce qui nous donne :
Soit :
Or, on sait que et que . De plus on remarque qu'en effectuant à nouveau une intégration par parties sur cette nouvelle intégrale apparue, on va ré-obtenir l'intégrale cherchée. On a alors :
Ainsi, on obtient :
Ce qui nous donne :
Or, on sait que et que . De plus on remarque {\color{blue}{\textbf{la présence de l'intégrale cherchée}}} . On a alors :
Finalement, on obtient :
Sur l'intervalle d'intégration , le terme est strictement positif. Donc , ce qui implique :
On a alors la séquence d'intégration suivante :
Ce qui nous donne :
Soit :
Or, on sait que et que . De plus on remarque qu'en effectuant à nouveau une intégration par parties sur cette nouvelle intégrale apparue, on va ré-obtenir l'intégrale cherchée. On a alors :
Ainsi, on obtient :
Ce qui nous donne :
Or, on sait que et que . De plus on remarque {\color{blue}{\textbf{la présence de l'intégrale cherchée}}} . On a alors :
Finalement, on obtient :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.