Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Vers la prépa (3) - Exercice 1
40 min
65
Un exercice classique de l'enseignement supérieur.
Question 1
On considère l'équation linéaire du premier ordre, à coefficients variables, avec second membre, suivante :
Chercher, sur , l'unique solution de qui satisfait à la condition .
Correction
L'équa
tion étant linéaire, la solution générale sera la somme de : ;
la solution homogène (ou sans second membre) de l'équation sans second membre. On la notera ;
la solution particulière (ou sans second membre) de l'équation globale. On la notera .
Recherche de a solution sans second membre, ou homogène.
On considère l'équation sans second membre suivante :
On a alors :
En primitivant, on trouve que :
Ainsi, on trouve que :
En posant , avec , on obtient :
Recherche de a solution particulière.
Le second membre étant un polynôme du troisième degré, nous allons donc choisir une solution particulière de la même nature. C'est pourquoi, avec les quatre nombres réels , , et , on pose :
Ainsi :
En simplifiant :
En regroupant les terme de même nature :
Soit :
Ce qui implique que :
On a alors :
Recherche de a solution globale.
Comme l'équation différentielle est linéaire, cela nous permet de dire que :
Donc :
Ce qui nous permet d'écrire :
On pose alors , on a alors la solution générale suivante :
Parmi toutes les solutions précédentes, une seule d'entre-elles satisfait à la condition . On a alors :
Ce qui nous permet d'écrire que :
Soit encore :
Le polynôme admet comme racine évidente . Ainsi, il est possible de factoriser par . On a alors :
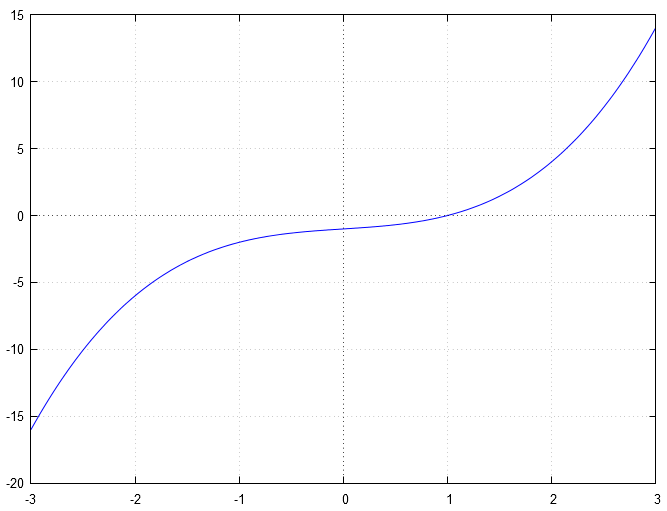
Finalement, on trouve que :
Ce qui nous donne graphiquement :
tion étant linéaire, la solution générale sera la somme de : ;
la solution homogène (ou sans second membre) de l'équation sans second membre. On la notera ;
la solution particulière (ou sans second membre) de l'équation globale. On la notera .
Recherche de a solution sans second membre, ou homogène.
On considère l'équation sans second membre suivante :
On a alors :
En primitivant, on trouve que :
Ainsi, on trouve que :
En posant , avec , on obtient :
Recherche de a solution particulière.
Le second membre étant un polynôme du troisième degré, nous allons donc choisir une solution particulière de la même nature. C'est pourquoi, avec les quatre nombres réels , , et , on pose :
Ainsi :
En simplifiant :
En regroupant les terme de même nature :
Soit :
Ce qui implique que :
On a alors :
Recherche de a solution globale.
Comme l'équation différentielle est linéaire, cela nous permet de dire que :
Donc :
Ce qui nous permet d'écrire :
On pose alors , on a alors la solution générale suivante :
Parmi toutes les solutions précédentes, une seule d'entre-elles satisfait à la condition . On a alors :
Ce qui nous permet d'écrire que :
Soit encore :
Le polynôme admet comme racine évidente . Ainsi, il est possible de factoriser par . On a alors :
Finalement, on trouve que :
Ce qui nous donne graphiquement :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.